|
|
[QUE/CM-07005]Node id: 2357page
| A simple pendulum, consisting of a mass $m$ and a weightless string of length $L$, is mounted on a support of mass $M$ which is attached to a horizontal spring with force constant $k$ as shown in figure below. Set up the Lagrangian and obtain the frequencies of small oscillations about the equilibrium position. |
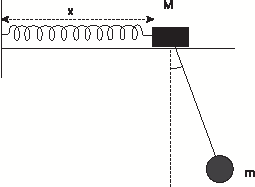 |
|

|
22-04-16 10:04:47 |
n |
|
|
[QUE/CM-02038] Bifilar PendulumNode id: 3106page |

|
22-04-16 10:04:26 |
n |
|
|
[QUE/CM-07004]Node id: 2358page
Three point like masses, all of them equal to $m$, and two massless springs (constant $k$) connecting them are constrained to move in a frictionless tube of radius $R$. The system is in gravitational field as shown in figure. The springs are of zero length and the masses may move through one another. Using Lagrangian methods, find the normal modes of small vibration about the position of equilibrium of this system and describe each of the modes.
|
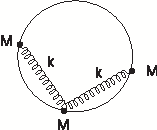 |
|

|
22-04-16 10:04:05 |
n |
|
|
[QUE/CM-07003]Node id: 2359page
|
A smooth uniform circular hoop of mass M and radius $R$ swings in a vertical plane about a point $O$ at which it freely hangs to a fixed support. A bead B of mass $M$ slides without friction on the hoop. Let $\theta$ and $\phi$ be the angles as shown in the Figure below.
- Set up the Lagrangian and find the equations of motion.
- Find the characteristic frequencies and the normal modes of smalloscillations about the position of stable equilibrium.
|
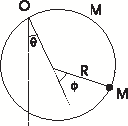 |
|

|
22-04-16 10:04:02 |
n |
|
|
[QUE/CM-10001] Canonical TransformationsNode id: 1956pageThe motion of a particle undergoing constant acceleration \(a\) in one dimension is described by
\begin{eqnarray*}
x &=& x_0 + \frac{p_0t}{m} + \frac{1}{2}a t^2\\
p&=&p_0+m a t
\end{eqnarray*}Show that the transformation from the present ``old'' variables \((x,p)\) to initial ``new'' variables \((x_0,p_0)\) is a canonical transformation
(a) by Poisson bracket test
(b) by finding ( for \(t\ne0\) ) the type 1 generating function \(F_1(x,x_0,t)\)
Source:Calkin
|

|
22-04-16 10:04:11 |
n |
|
|
[QUE/CM-08009] Counting Number of Degrees of Freedom of a Rigid BodyNode id: 3118page
- Consider a system of three point masses connected by rigid rods. Find the number of constraints and hence the number of generalized coordinates required for this system when the masses do not lie in a straight line.
- Next repeat the above problem for three three masses constrained to lie in a straight line.
- Count the number of constraints and hence find the number of degrees of a freedom of a rigid body consisting of \(n\) point masses separated by fixed distances. Compute the value of number of degrees of freedom for a few values of \(n\) . What happens when \(n\) is very large?
A useful reference for counting of degrees of freedom for a rigid body, in a manner described above, is
Jorge Bernal et al., "Exact calculation of the number of degrees of freedom of a rigid body constituted by n particles". arXiv:1002.2002v1 (Feb9,2010)
|

|
22-04-16 09:04:30 |
n |
|
|
[QUE/QFT-06004] Node id: 3508pageDoes there exist an invertible matrix \(S\) such that \[ S \gamma_\mu S^{-1} = \gamma_\mu'\] where \[\gamma_1'= \gamma_2\gamma_3, \quad \gamma_2'=\gamma_3\gamma_1, \quad \gamma_3'= \gamma_1\gamma_2, \gamma_4'=\gamma_5 \gamma_4?\]
|

|
22-04-16 09:04:18 |
n |
|
|
[QUE/EM-02003] Sixteen charges on a regular polygonNode id: 2625pageSixteen equal charges $q$ are placed at the corners of a regular polygon of 17 sides. Find the force exerted by these charges on a seventeenth charge $q$ placed at the center of the polygon.
|

|
22-04-16 09:04:54 |
n |
|
|
[QUE/QM-10012]Node id: 2781pageIn the position representation a function of \(\vec{r}\), \(f(\vec{r})\), can be thought of as an operator \(\hat{f}\): \[ \hat{f} \psi(\vec{r}) = f(\vec{r}) \psi(\vec{r}). \] Use spherical harmonics, \(Y_{\ell m}(\theta, \phi)\) to define operators \(\widehat{Y}_{\ell m}\) in the above sense. Use properties of spherical harmonics and known expressions for angular momentum operators in polar coordinates to show \begin{eqnarray} [L_z, \widehat{Y}_{\ell m}] &=& m\hbar\, \widehat{Y}_{\ell m}, \nonumber\\{} [L_{\pm}, \widehat{Y}_{\ell m}] &=& \sqrt{\ell(\ell+1) - m(m\pm1)}\,\hbar\,\widehat{Y}_{\ell\pm 1 m}.\nonumber \end{eqnarray}
|

|
22-04-15 20:04:41 |
n |
|
|
[QUE/VS-02006]Node id: 3708pageQUE/VS-02006
- Consider the vector space of all real numbers with field of all real numbers. Is the set \(\{1, \sqrt{2}\}\) linearly independent? Does it form a basis? Give an explanation of your answer.
- Let \(V\) be the vector space of all real numbers with the set \(Q\) as the field. Is the set \(\{1,\sqrt{2}\}\) linearly independent? Why? Does it form a basis?
|

|
22-04-15 20:04:29 |
n |
|
|
Testing Links inside Embedded Viewed Page Node id: 1474page |

|
22-04-15 16:04:35 |
n |
|
|
[2019CM/HMW-01] Tutorial I Node id: 3066page |

|
22-04-15 15:04:14 |
n |
|
|
[2019QM/HMW-01] Tutorial -INode id: 3064page |

|
22-04-15 15:04:47 |
n |
|
|
[NOTES/ODE-02003] Series Solution Case-IIINode id: 1752page |

|
22-04-15 15:04:00 |
n |
|
|
[NOTES/ODE-02002] Series Solution Case-IINode id: 1751page |

|
22-04-15 15:04:55 |
n |
|
|
[NOTES/ODE-02001] Series Solution Case-INode id: 1750page |

|
22-04-15 15:04:56 |
n |
|
|
[2013]Node id: 5373page |

|
22-04-15 14:04:43 |
n |
|
|
Unbounded Intervals and Use of Fourier TransformNode id: 1747pageWe illustrate use of Fourier transform for problems involving infinite domains with example of free particle time dependent Schrodinger equation.
|

|
22-04-15 14:04:06 |
n |
|
|
[NOTES/ODE-02005] Frobenius Method of Series SolutionNode id: 1749page |

|
22-04-15 14:04:52 |
n |
|
|
[NOTES/ODE-01001] Equations with Constant CoefficientsNode id: 1748page |

|
22-04-15 14:04:09 |
n |