|
|
[2013EM/HMW-06]Node id: 5380page |

|
22-04-17 09:04:45 |
n |
|
|
[2013EM/HMW-04]Node id: 5378page |

|
22-04-17 09:04:12 |
n |
|
|
[2013EM/HMW-03]Node id: 5377page |

|
22-04-17 09:04:54 |
n |
|
|
[2013EM/HMW-02]Node id: 5376page |

|
22-04-17 09:04:01 |
n |
|
|
[2013EM/HMW-01]Node id: 5375page |

|
22-04-17 08:04:36 |
n |
|
|
QM-22 WKB ApproximationNode id: 764pageExercises
This set has practice problems on WKB approximation for bound state energy levels.
qm-exe-22001
|

|
22-04-17 06:04:24 |
n |
|
|
[QUE/CM-02037] An Uphill ProblemNode id: 3105pageWatch the yoututbe video.
https://www.youtube.com/watch?v=SUjY0sdtGus
- Describe what you see in the video.
- Set up the Lagrangian for (a) cylinder, (b) a double cone, rolling on the rails.
- Solve the equations of motion and show that the cylinder climbs down while the double cone will climb up the rails.
|

|
22-04-16 13:04:45 |
n |
|
|
[QUE/CM-09001] Node id: 2207page
Show that the kinetic energy of a uniform rod of mass \(m\) is
\[ T = \frac{1}{6}m(\vec{u}.\vec{u} + \vec{u}.\vec{v}+\vec{v}.\vec{v} )\]
where \(\vec{u}\) and \(\vec{v}\) are the velocities of the two ends.
Woodhouse
|

|
22-04-16 11:04:00 |
n |
|
|
[QUE/CM-07010] Small Ocillations and He moleculeNode id: 2238pageAssuming that the van der Waals force between two He atoms is described by Lenard Jones potential
\[ V(r) = \epsilon_0 \Big( \frac{r_0^{12}}{r^{12}}- \frac{r^6_0}{r^6}\Big)\]
and that \(\epsilon_0=1.42\times10^{15} \text{erg},\qquad r_0= 2.87\times10^{-8}\text{cm}\).
Determine
- the force constant for small oscillations
- the fequency of oscillations for the vibrational motion of a bound pair of He atoms.
- Using the approximate results obtained above and quanum mechanical expression for vibrational energy of He molecule, determine whether or not two He atoms canform a molecule He\(_2\). ( Note that these results are only approximate (and can in fact lead to the worng conclusion!) but nevetheless they are instructive. Can you guess why the result might be wrong?
Atlee Jackson*
|

|
22-04-16 11:04:54 |
n |
|
|
[QUE/CM-07011] Small Oscillations of Oxygen MoleculeNode id: 2239pageAssuming that the van der Waals force between two oxygen atoms is described by Lenard Jones potential \[ V(r) = \epsilon_0 \Big( \frac{r_0^{12}}{r^{12}}- \frac{r^6_0}{r^6}\Big)\]
and that \(\epsilon_0=16.4\times10^{15}\) \text{erg}, r_0= 3.88\times10^{-8}\text{cm}\) determine
- the force constant for small oscillations
- the fequency of oscillations for the vibrational motion of a bound pair of He atoms.
- Using the approximate results obtained comote the numerical value of the vibration of oxygen molecule. How do explain the differences between your answer and the experimenl value \(\nu=6.45\times10^{13}\).
Atlee Jackson*
|

|
22-04-16 11:04:54 |
n |
|
|
[QUE/CM-08001]Node id: 2348pageA mass point $M$ is moving under gravity along a rod, which rotates about the vertical axis passng through the fixed end of the rod. The angle between the rod and the vertical axis remains constant equal to $\alpha$.
- Set up the Newtonian equations of motion
- Set up the Lagrangian and obtain the equations of motion.
- Discuss the motion using the generalized coordinates in (b).
[SDG]
|

|
22-04-16 11:04:31 |
n |
|
|
[QUE/CM-08003]Node id: 2350pageA perfectly smooth horizontal disk is rotating with an angular velocity $\omega$ about a vertical axis passing through its center. A person on the disk at a distance $R$ from the origin gives a perfectly smooth coin (negligible size)pf mass $m$ a push towards the origin. This push gives it an initial velocity $V$ relative to the disk. Show that the motion for a time $t$, which is such that $(\omega t)^2$ is negligible, appears to the person on the disk to be a parabola, and give the equation of the parabola.
[Lim 1098]
|

|
22-04-16 11:04:46 |
n |
|
|
[QU/CM-08002]Node id: 2349pageConsider a hoop of radius $a$ in a vertical plane with angular velocity $\omega$ about the vertical diameter. Consider a bead of mass $m$ which slides without friction on the hoop as indicated in figure.
Under what condition will the equilibrium of the bead at $\theta=0$ be stable?
- Find another value of $\theta$ for which, in certain circumstances, the bead will be in stable equlibrium. Indicate the values of $\omega$ for which this stable equilibrium takes place.
- Explain your answer with the aid of appropriate graphs of the potential energy versus $\theta$ as measured in the rotating frame. [Lim 1097]
Problem-CM-08002
|

|
22-04-16 11:04:23 |
n |
|
|
[QUE/CM-07006]Node id: 2356pageA thin uniform bar of mass $m$ and length \(\frac{3L}{2}\) is suspended by a spring of length \(L\) and force constant \(k\) and negligible mass. Find the normal frequencies and normal modes of small oscillations in a plane.
|

|
22-04-16 11:04:19 |
n |
|
|
QUE/CM-07009] A small oscillation problem in two dimensionsNode id: 2355page
|
Consider a particle of mass \(m\) moving in two dimensions in a potential \[ V(x,y) =
\frac{k}{2}(5 x^2 + 2 x y + 5 y^2)\]
- At what point \((x_0,y_0)\) is the particle in stable equilibrium?
- Give the Lagrangian appropriate for small oscillations about this equilibrium position.
- Find the normal frequencies of vibration in (b).
- Write the Lagrangian in terms of normal coordinates and verify that it takes the form \[\mathscr{L} = \frac{1}{2}(\dot{Q}_1^2 + \dot{Q}_2^2) -\frac{1}{2}( Q_1^2 + Q_2^2)\]
|
|

|
22-04-16 11:04:09 |
n |
|
|
[QUE/CM-08004]Node id: 2708pageLet A be a real antisymmetric matrix.
- Show that $|I\,+\,A| $ is nonsingular.
- Show that $$ B\ =\ (I\,+\,A)(I\,-\,A)^{-1} $$
an orthogonal matrix.
|

|
22-04-16 11:04:00 |
n |
|
|
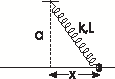
[QUE/CM-07001] Node id: 2351page
|
The figure shows a body of mass $m$ constrained to move in a
horizontal line under the influence of a massless spring of
natural length \(L\) and spring constant $k$. Find the equilibrium
points for the following three cases.
- Case \(a=L\): When the mass is at $x=0$, the spring is at its equilibrium length.
- Case \(a>L\): When $x=0$, the spring is stretched.
- Case \(a < L\): When $x=0$, the spring is compressed.
- Find the period of small oscillations in case (a).
|
 |
|

|
22-04-16 11:04:02 |
n |
|
|
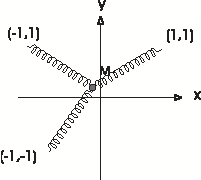
[QUE/CM-07002] Three Springs ProblemNode id: 2352page
Three massless springs of natural length $\surd 2$ and spring constant
$k$ are attached to a point particle of mass $m$ and to the fixed
points $(-1,1), (1,1)$ and $(1,1)$ as shown in the Fig. 1. The point
mass is allowed to move in the $(x,y)$ plane only.
- Write the Lagrangian for the system.
- Is there an equilibrium position for the point mass? Where is it?
- Give the Lagrangian appropriate for small oscillations.
- Find the frequencies and normal coordinates of small oscillations.
- Sketch the normal modes.
|
 |
|

|
22-04-16 11:04:51 |
n |
|
|
[QUE/CM-07007] Double Pendulum Node id: 2353page
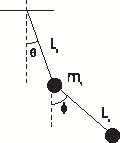 |
Set up the Lagrangian for double pendulum consisting of two masses $m_1$ and $m_2$ connected to light bars of lengths $l_1$ and $l_2$ as shown in figure. Find the frequencies of small oscillations for the case of equal masses, $m_1=m_2$ and equal lengths $l_1=l_2.$
|
|

|
22-04-16 11:04:32 |
n |
|
|
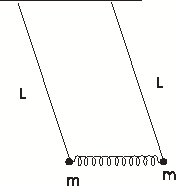
[QUE/CM-07008]Node id: 2354page
Consider two simple pendula each of mass $m$ and length $L$ joined by a massless spring with constant $k$ as shown in the figure.The distance between the pivots is chosen so that the spring is unstretched when the pendula are vertical. Find the frequencies and the normal modes of oscillations of this system about the equilibrium.
|
 |
|

|
22-04-16 10:04:54 |
n |