|
|
[YMP/EM-02012] Average Value of Electric FieldNode id: 6021pageProblem
A solid sphere of radius \(R\) carries a charge density \(\rho(\vec{r})\). Show that the average of the electric field inside the sphere is \[\vec{E}= - \frac{1}{4\pi\epsilon_0} \frac{\vec{p}}{R^3},\] where \(\vec{p}\) is the total dipole moment of the sphere. |
|
23-11-23 22:11:27 |
n |
|
|
[YMP/EM-02011] Overlapping Spheres -IINode id: 6024article
Problem
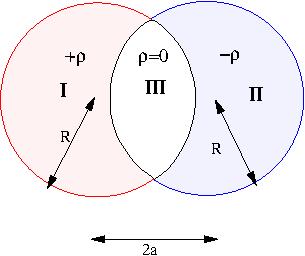
Two spheres each of radius $R$ are placed so that they partially overlap. The charge densities in the overlap region is zero and in the two non overlapping regions is $+\rho$ and $-\rho$ respectively as shown in figure. The separation between the centers of the spheres is $D$.Find the electric field in the two non-overlap regions. |
 |
|
|
23-11-23 22:11:38 |
n |
|
|
[YMP/EM-02009] Electric Field of a Uniformly Charged SphereNode id: 6022page
|
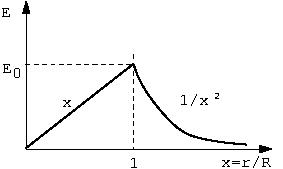
Show that the electric field of a uniformly charged sphere, radius \(R\), total charge \(Q\) has the magnitude given by\[E= \begin{cases} E_0 x & x< 1 \\ E_0/x^2 & x>1 \end{cases}\]where \(E_0= \dfrac{Q}{4\pi\epsilon_0 R^2 }\) and \(x=\dfrac{r}{R}\).
|
|
\(\newcommand{\Prime}{{^\prime}}\) |
|
23-11-23 22:11:47 |
n |
|
|
[YMP/EM-02008] Electric Field Due to a DipoleNode id: 6013pageA dipole is a system of two equal and opposite charges separated by a distance. Its electric field is computed and the field at large distances depends only on the dipole moment, defined as the product of the charge and separation between the charges.
While dipole is a system of two charges, the concept of dipole moment is defined and is useful for any system of charges with total zero charge. |
|
23-11-23 22:11:57 |
n |
|
|
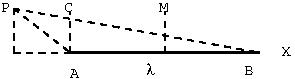
[YMP/EM-02004] Electric Field due to a Line with Uniform Charge DensityNode id: 6016pageLet \(AB\) be a line charge with charge per unit length $\lambda$, which is given to be uniform. The field is to be computed at a point \(P\),. Let \(p\) be the perpendicular distance of \(P\) from the line \(AB\). let \(\alpha, \beta\) be the angles as shown in the figure. Electric field will be calculated at a general point \(P\), the corner point \(C\) and the middle point \(M\) as shown in figure below.
|
|
23-11-23 22:11:35 |
n |
|
|
[YMP/EM-02003] Dipole Moment of Overlapping SpheresNode id: 6015page
| Two spheres each of radius $R$ are placed so that they partially overlap. The charge densities in the overlap region is zero. Outside the overlap region but inside the spheres the charge densities in the two non overlapping regions are $+\rho$ and $-\rho$, respectively, as shown in figure. The charge density in the overlap region will be zero. The separation between the centers of the spheres is $D$. |
|
- Guess the value of the dipole moment?
- Compute the dipole moment of the system and check the correctness of the expression you guessed.
- How will the dipole moment change if the two spheres equal and opposite total charges but have different radii \(a,b, a \ne b\).
|
|
23-11-23 22:11:53 |
n |
|
|
[YMP/EM-04008] Force Between the Hemispheres Parts of a Uniformly Charged SphereNode id: 5929pageA conducting spherical shell of radius \(R\) is placed in a uniform electric field along the \(Z\)- axis.A plane perpendicular to the electric field divides the shell into two equal halves. Show that the Coulomb force acting on the hemispherical surfaces which tends to separate them is across the diametral plane perpendicular to \(\vec E\) is given by
\[ F = \tfrac{9}{4}\pi \epsilon_0 R^2 E_0^2\] |
|
23-11-22 12:11:47 |
n |
|
|
[YMP/EM-04006] Point Charge and an Infinite PlaneNode id: 5927pageProblem
A point charge is placed at a distance \(d\) from an infinite grounded
conducting plane sheet. Assuming the standard image charge, find
- induced surface charge density. Show that the total induced charge is equal to−q
- find the potential due to the induced charge;
- using Coulomb's law, find the force between the charge and conducting sheet making use of the induced surface charge density on the plane.
\(\newcommand{\pp}[2][]{\frac{\partial #1}{\partial #2}}\) |
|
23-11-22 12:11:19 |
n |
|
|
[YMP/EM-04005] Using Maxwell Stress TensorNode id: 5926pageDerive the Coulomb force due to a static charge on another static charge using the Maxwell stress tensor. |
|
23-11-22 11:11:30 |
n |
|
|
[YMP/EM-04003] Electrostatic energy of a point charge and a grounded infinite conducting plane. Node id: 5924pageProblem:
What is the electrostatic energy of a point charge placed near an grounded infinite conducting plane. Show that this is not equal to the energy of the point charge and it image. |
|
23-11-22 11:11:19 |
n |
|
|
[YMP/EM-04004] Grounded Conducting Sphere in Uniform Electric Field Node id: 5925pageThe problem of a conducting sphere in a uniform electric field is solved. Unlike many other problems, in this problem the potential does not go to zero as $\longrightarrow \infty$. |
|
23-11-21 22:11:49 |
n |
|
|
[YMP/EM-04001] Grounded Conducting Sphere and a Point Charge Node id: 5923pageTwo point charges \(Q\) and \(Q^\prime\) are located at positions given by \(\vec{a}, \vec{b}, (a\ne b) \). Find the conditions on \(Q, Q^\prime, a, b \) so that the potential on the surface of a sphere of radius \(R\) with center at the origin may be zero.
Note the result of this problem is used in solution for electric potential of a grounded conducting sphere in presence of a point charge by the method of images. |
|
23-11-20 22:11:46 |
n |
|
|
[QUE/EM-ALL] Repository of EM Theory Problems and QuestionsNode id: 5841pageThis repository is a collection of PROBLEMS and QUESTIONS in Electromagnetic Theory.
These are arranged according to topics in the subject.
Not sorted, or arranged, in any particular order within a topic.
Suitable for teachers and content developers only.
Click on any topic to browse all available problems.
(Click opens an embedded window) |
|
23-11-20 20:11:51 |
n |
|
|
[NOTES/EM-ALL] Repository of EM Theory NOTESNode id: 5987pageThis is a repository of NOTES in EM-Theory.
Recommended only for authors and content developers.
Not useful for visitors looking for study material.
|
|
23-11-20 18:11:16 |
n |
|
|
[NOTES/EM-01009] From Action at a Distance to Field ConceptNode id: 5952page
The concept of electric field to describe the interaction of charged particles is briefly explained. Instead of the Coulomb interaction, which is an instantaneous action, we say a charge produces electric field which in turn acts on another charge present at some other point. Similarly the magnetic force on a current, or a moving charged particle is described in terms of magnetic field produced by a magnet or a current..
|
|
23-11-10 11:11:46 |
n |
|
|
Jumping RIngsNode id: 6011video_page |
|
23-11-10 06:11:59 |
n |
|
|
Jumping RIngsNode id: 6010video_page |
|
23-11-10 06:11:54 |
n |
|
|
[NOTES/EM-01007] Using dimensional Analysis to get Quick Numerical EstimatesNode id: 5950pageBy means of a few examples we show how dimensional analysis can be used to quickly estimate numerical values of expressions occurring in problems. |
|
23-11-09 20:11:52 |
n |
|
|
[LECS/EM-01003] Motion of Charges in Electric and Magnetic FieldsNode id: 6003pageSeveral examples of motion of charges in electric and magnetic fields are presented. |
|
23-11-07 23:11:14 |
n |
|
|
[NOTES/EM-01013] SI System of UnitsNode id: 6005pageThe Si system of units are explained. This is the system that will be used everywhere in the resources of Proofs program. |
|
23-11-07 09:11:39 |
n |
||Message]