[YMP/EM-04005] Using Maxwell Stress Tensor

Solution

Coming back to problem, the force can be computed  by integrating Maxwell's stress tensor over a surface enclosing the second charge. The choice of surface is arbitrary and is decided by the convenience of doing the surface integral. Consider two charges \(\pm q\) separated by a distance \(2a\). Consider a hemispherical surface of radius \(R\) enclosing the second charge and having its centre midway between the charges as shown in figure

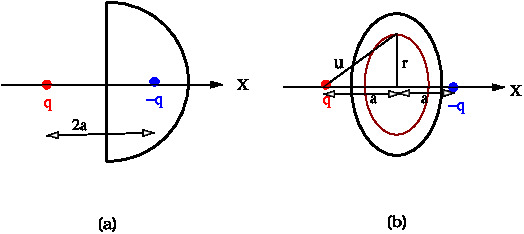
We  will take the limit \(R \to \infty\). In this limit the curved surface does not contribute to the surface integral. This is because at large  distance the surface area increases like \(R^2\). The electric field of the two charges, ( in our case, equal and opposite charges \(\pm q\)), goes to zero faster than  \(1/R^2\) and the stress tensor decreases faster than \(1/R^4\) for \(R\to \infty\). The total electric field is along the \(X\)-axis, the \(y\) and \(z\) components are zero. Hence we need to compute the only \(xx\) component of the stress tensor. \begin{equation} T_{xx} = \epsilon_0(E_x^2 - (1/2)E^2) = \frac{\epsilon_0}{2} E_x^2 \end{equation} Divide the circular base of the hemisphere into thin rings of radius \(r\). The \(x\)- component of electric field at points on the ring is \begin{equation} E_x = -\frac{2q}{4\pi\epsilon_0}\frac{a}{u^3}   \end{equation} where \(u^2=r^2+a^2\). The contribution of one such ring to the force is
 \begin{eqnarray}\nonumber
  F_x &=& -\iint T_{xx} dS\\\nonumber
  &=& - \int_0^\infty  \frac{1}{2}\epsilon_0 E^2 (2\pi r dr).\\\nonumber
  &=& -\frac{1}{2}\epsilon_0 \frac{4q^2a^2}{(4\pi\epsilon_0)^2} \int_0^\infty\frac{2\pi r \,dr}{u^6}\\\nonumber
  &=& -\frac{q^2a^2}{4\pi\epsilon_0}\int_a^\infty \frac{du}{u^5} \qquad \because \quad u^2 = r^2+a^2\\\nonumber
  &=& -\frac{q^2}{4\pi\epsilon_0}\frac{1}{4a^2}
 \end{eqnarray}
 Question for you: What changes will be needed in the above solution if we had started with two charges  \(q\) and \(q^\prime\ne -q\)?