|
|
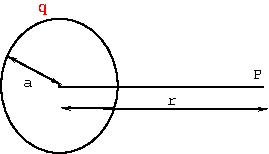
[YMP/EM-02007] Electric Field of a Uniformly Charged Spherical ShellNode id: 6020pageWe will show that for a uniformly charged sphere, radius \(a\) and charge \(Q\),
the electric field is given by
\begin{equation}
\vec E = \begin{cases} 0 & \text{if } r<a\\
\frac{Q}{4\pi\epsilon_0 R^2 } & \text{if } r > a
\end{cases}
\end{equation} |
 |
|

|
23-12-18 12:12:25 |
n |
|
|
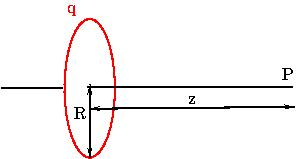
[YMP/EM-02005] Field due to a Uniformly Charged RingNode id: 6018pageThe electric field due to a charged ring, at a point, \(P\) on its axis, is computed using Coulomb's law. We will show that the electric field of uniformly charged ring, radius \(R\), at a point on the axis of the ring, is given by
\begin{equation}
\vec E = \frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \, \hat k.
\end{equation}
where \(q\) is the total charge and \(z\) is the distance if field point from the center of the ring. |
 |
|

|
23-12-18 11:12:07 |
n |
|
|
[2015MeOW/HMW--Archive] @BITS Hyderabad, Every One in BTech Class has a Different Home Work PaperNode id: 3148pageThis set of homework assignments were prepared for
First Semester Course MeOW (Mechanics, Oscillations, and Waves)
2015 Batch of B.Tech program at BITS-Pilani University Hyderabad (July-Nov 2015).
More than 700 different question papers and answer sets were generated by
an automated process for a class of 700 students.
Each student was given a different set of question paper for home work.
The students were asked to submit their answers online.
The evaluation of answers was also automated.
The process tested automation of generating the ranking type of question papers and evaluation.
It is possible to extend it to other types of questions and is likely to be useful for large classes.
|

|
23-12-17 10:12:43 |
n |
|
|
[PROFILE/AKK] ResumeNode id: 6034page |

|
23-12-17 04:12:54 |
n |
|
|
[CRT/MM-18001] Curated Resources --- Dirac Delta Function Node id: 6033curated_contentWORK ON THIS PAGE IS IN PROGRESS Last Update : December 15, 2023
|

|
23-12-15 20:12:00 |
n |
|
|
DD-01 Dirac Delta FunctionNode id: 1230pageThis write up is contributed by Prof. Pankaj Sharan as a part of lectures on electrodynamics.
For full set of eight lectures click here
|

|
23-12-15 20:12:08 |
n |
|
|
PROFILE-AKK-QHJ-BookNode id: 6032page |

|
23-12-13 20:12:49 |
n |
|
|
PROFILE-AKK-TEACHING EXPERINCENode id: 6031page |

|
23-12-13 19:12:53 |
n |
|
|
PROFILE-AKK-BOOKSNode id: 6030page |

|
23-12-13 19:12:26 |
n |
|
|
Proofs Warehouse - Collection III Utilities For LearningNode id: 3886collection |

|
23-12-12 11:12:59 |
n |
|
|
How to check if derivative of a function with respect to a complex variable exists?Node id: 5784basic_multi_stepMethods to check if a function has a derivative at a point.
I- Using the definition
II- Using properties of derivative
III- Using Cauchy Riemann Equations
What will not be done here :-
The functions with branch point singularity will be discussed separately
$\newcommand{\pp}[2][]{\frac{\partial #1}{\partial #2}}$
|

|
23-12-12 11:12:39 |
n |
|
|
[YMP/EM-01005] Alpha Particle in Magnetic Field --- Circular OrbitNode id: 5902page |

|
23-12-12 11:12:36 |
n |
|
|
[2023CNG/QM-ALL] Collection of Resources for (CNG) Online Course on Quantum Mechanics 2023Node id: 5879collectionABOUT THIS COLLECTION
This is a collection of links to all resources, lectures, video recordings
and Extra study material for 2023 ONLINE COURSE ON Quantum Mechanics.
Click here To learn more about the course
|

|
23-12-12 11:12:26 |
n |
|
|
Matrices --- 150 Problem Sets for DiagonalizationNode id: 959pageThis sample contains 150 sets of $3\times 3$ matrices for computing eigenvectors and eigenvalues.
Why so many sets?
The primary reason for creating so many sets was to give each students a different assignment and to give them extra sets for practice purposes.
How were these sets generated?
A large number $3\times3$ of matrices were generated starting with the Jordan canonical form with diagonal entries varied over a range of values. Then a similarity transform was applied by number of different sets of invertible matrices on each one of the matrices in Jordan form. Finally, those problems were discarded where the matrices, or the eigenvalues, or the eigenvectors had some large elements. Mathematica was used to write the $\LaTeX$ code of the matrices, their eigenvalues and eigenvectors.
One $\LaTeX$ file was generated for each matrix and stored. These were then input in a main $\LaTeX$ file which generated the final PDF file of all sets with all answers at the end.
|

|
23-12-12 06:12:05 |
n |
|
|
[LECS/EM-02001] Coulomb's Law and Electric FieldNode id: 6012articleThe Coulomb's law gives the force between two point charges. It can be reformulated as giving electric field of a point charge which in turn gives rise to force on a nearby point charge.The electric field of a point charge is generalized to system with continuous charge distributions. Expressions for the electric field of line surface and volume charge distriibutions are given.
|

|
23-12-12 05:12:28 |
n |
|
|
[YMP/EM-All] Solved Problems in Electromagnetic TheoryNode id: 5918collectionWork Under Progress
(LUPDate : Nov 24, 2023)
|

|
23-12-11 16:12:24 |
n |
|
|
What horrible things we allow our children to be taught --- A Sample!!Node id: 6029blogHere is a sample of horrible Physics and Mathematics our children learn from established centers.
We pay them for our children to learn horrible "Physics and Mathematics".
Snap shot taken from https://byjus.com/physics/maxwells-equations/#
Refresh the page, if you do not see the body of this page
|

|
23-12-11 06:12:16 |
n |
|
|
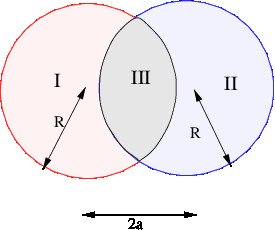
[YMP/EM-02010] Electric Field of Overlapping Uniformly Charged SpheresNode id: 6023page
|
Problem
Two spheres, each of radius $R$ and carrying charge densities $+\rho$ and $-\rho$ respectively, are placed so that they partially overlap. The separation between the centers of the spheres is $D$. Show that the field in the region of overlap is constant and find its value. |
 |
|

|
23-12-04 05:12:08 |
n |
|
|
[Feyn-II-Sec14]Node id: 6026page |

|
23-11-24 10:11:27 |
n |
|
|
[YMP/EM-02012] Average Value of Electric FieldNode id: 6021pageProblem
A solid sphere of radius \(R\) carries a charge density \(\rho(\vec{r})\). Show that the average of the electric field inside the sphere is \[\vec{E}= - \frac{1}{4\pi\epsilon_0} \frac{\vec{p}}{R^3},\] where \(\vec{p}\) is the total dipole moment of the sphere.
|

|
23-11-23 22:11:27 |
n |