Browse & Filter

List all the elements of symmetries of a square and construct the
group multiplication table. Use the multiplication table construct the class
multiplication rules.}

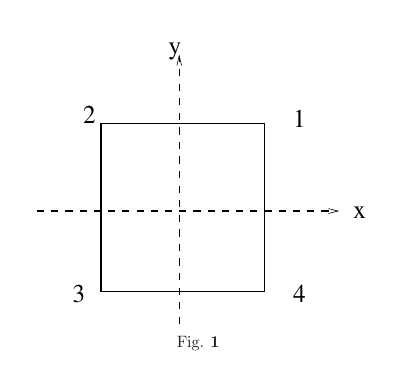
Notation:Name  the group elements as follows.

The classes are given to be\\
\begin{equation*} \begin{array}{ll} C_1=\{e\}.&  \\ C_2 =\{4_z^2\} &C_3 =\{4_z,
4_z^3\} \\ C_4=\{m_x, m_y\} &C_5 =\{m_{13}, m_{24}\} \end{array}\end{equation*}

In \(C^3\) with scalar product \((x,y)=x^\dagger y\) find the adjoint of operator \(A\) where \(A\) is defined to be
\begin{equation}
    A  \begin{pmatrix}x_1\\ x_2\\ x_3 \end{pmatrix}
     = \begin{pmatrix}x_1+ x_2\\ x_2+x_3 \\ x_3+x_1\end{pmatrix}
\end{equation}

Consider the vector  space of all polynomials \(p(t)\) of degree less than or 5 with inner product
\[((p,q) = \int_{-1}^1 p(t) q(t) \, t^2\, dt \]  Is the operator \[ A p(t) = \frac{ d p(t)} {dt}\]
self adjoint?

The matrix of a linear operator \(A\) in an orthonormal basis \(\{e_1, e_2,
e_3\}\) is given to be
\begin{equation}
  \underline{\sf A} = \begin{pmatrix}
                        0 & 1 & 0 \\
                        0 & 0 & 1 \\
                        1 & 0 & 0
                      \end{pmatrix}
\end{equation}
Is this operator unitary? How is the basis \(\{f_1, f_2,f_3\}\)
 in which the operator is diagonal related to \(\{e_1, e_2,e_3\}\)?

The classes of the permutation group  $S_3$ are given to be $$ C_0 =\{e\}, C_1=\{(1,2),(1,3),(2,3)\}, C_2 = \{(1,2,3),(1,3,2)\} $$ Express $C_1^2,C_2^2$ and $C_1 C_2$  in terms of the classes and find the class constants.

What is the number of irreducible representations of the D-4 group.
Find their dimensions and construct the character table for the group.
You may use the notation and information given below.}

The classes are given to be  \begin{equation*}  \begin{array}{ll} C_1=\{e\}.&  \\
C_2 =\{4_z^2\} &C_3 =\{4_z, 4_z^3\} \\
C_4=\{m_x, m_y\} &C_5 =\{m_{13}, m_{24}\}
\end{array}

You may use class multiplication rules \begin{equation*}  \begin{array}{llll}
C_2^2=C_1         & C_2C_3=C_3    & C_2C_4=C_4 & C_2C_5 = C_5\\
C_3^2 = 2C_1+C_2  & C_3C_4= 2C_5  & C_3 C_5 = 2C_4 &\\
C_4^2 =2C_1+2C_2  & C_4 C_5= 2C_3  &&\\
C_5^2= 2C_1+2C_2  &&&
\end{array} \end{equation*}

Consider the set of all vectors \(\xi=(\xi_1,\xi_2,\xi_3)\) in \(\C^(3)\) for
which

In which of the  above  cases do the set of all vectors form \(\xi\) form a vector
space?

Find all subgroups of the group of permutations $S_3$ on three objects.
For each subgroup check if it is an invariant subgroup.
For each class, explicitly verify the result that every invariant subgroup
either contains all elements of the class, or else is disjoint from the class.

In vector space of square integrable functions an operator \(T\) is defined as \[ T f(x)=\frac{1}{\sqrt{2}} f(2x+3)\] Find \(T^\dagger\) and check if \(T\) is (i) hermitian, (ii) unitary.