|
|
[2010QM01/HMW -- Archive] Summer Course@University of HyderabadNode id: 3427curated_contentContents
HomeWork: Matrix EIgnevalues EIgenvectors
WbQuest : Numerical Comparison of H Bohr's Theory with Precise Experimental data
Tutorial-I: Postulates of Quantum Mechanics
Tutorial-II: Calculating Commutators
Tutorial-III: Simultaneous Measurement, Uncertainty
Tutorial-IV: Uncertainty Principle
Tutorial-V: Matrix Elements Using Algebraic Methods
Tutorial-VI: Coordinate and Momentum Space Wave Functions
Tutorial-VII: Potential Problems in One Dimension
Tutorial-VIII: Potential Problems in One Dimension
Tutorial-IX: Reflection and Transmission in One Dimension
Tutorial-X: Time Development
Solved Examples-I: Dirac \(\delta\) function potential
|

|
22-04-26 11:04:38 |
n |
|
|
[2018CM/HMW -- Archive] Summer Course @ University of HyderabadNode id: 2111curated_content |

|
22-04-26 11:04:31 |
n |
|
|
[2019QM01/HMW -- Archive] Summer Course @ University of HyderabadNode id: 3434curated_content |

|
22-04-26 10:04:53 |
n |
|
|
[2018QM01/Eval -- Archive]-- Quiz, Test and Examination Papers --- Summer Course @ University of HyderabadNode id: 3412curated_content |

|
22-04-26 10:04:18 |
n |
|
|
[2018QM01/HMW -- Archive] Summer Course @ University of HyderabadNode id: 3408curated_content |

|
22-04-26 10:04:14 |
n |
|
|
[2018CM/LNNP-Archive] --- Summer Course @ University of HyderabadNode id: 3415curated_content |

|
22-04-26 10:04:14 |
n |
|
|
[2018QM01/LNP-Archive] --- Summer Course @ HCU Node id: 3411curated_content |

|
22-04-26 10:04:44 |
n |
|
|
[2018CM/TEST-01] Classical Mechanics Node id: 2127article
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:56 |
n |
|
|
[2018CM/FINAL-01] Classical Mechanics (2018)Node id: 2125article
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:50 |
n |
|
|
[2018CM/HMW-02]Classical Mechanics Node id: 2120pageClassical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:28 |
n |
|
|
[2018CM/HMW-03] Classical Mechanics Node id: 2122articleClassical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:06 |
n |
|
|
[2018CM/HMW-04] Classical Mechanics (2018) Node id: 2123article[toc:0]
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:53 |
n |
|
|
[2018CM/HMW-05] Classical Mechanics Node id: 2124article[toc:0]
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:42 |
n |
|
|
[2018CM/HMW-06] lassical Mechanics Node id: 2121article[toc:0]
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:39 |
n |
|
|
[2018CM/QUIZ-01] Classical Mechanics Node id: 2128article[toc:0]
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:23 |
n |
|
|
[2018CM/QUIZ-02] Classical Mechanics Node id: 2126article
Classical Mechanics (2018) :: A Course Given at University of Hyderabad
Assignments, Quiz, Test and Examination Paper
|

|
22-04-26 09:04:02 |
n |
|
|
2019-CM-I @ CMI :: Exam-Papers, Solutions Node id: 3278curated_content |

|
22-04-26 09:04:45 |
n |
|
|
[2019EM/HMW-06]Node id: 5368pageElectrodynamics Oct 17, 2018
Tutorial-V (VI)
- A cylindrical resistor of length \(\ell\), radius \(a\) and resistivity $\varrho$ carrying a current \(i\).
- Show that the Poynting vector $\vec{S}$ at the surface of the resistor is everywhere directed to the normal to the surface, as shown,
- Show the rate $\rho$ at which energy flows into the resistor through its cylindrical surface, calculated by integrating the Poynting vector over this surface, is equal to the rate at which Joule heat is produced, i.e. \begin{equation*} \int\vec{S}\cdot\vec{dA}=i^2R \end{equation*}
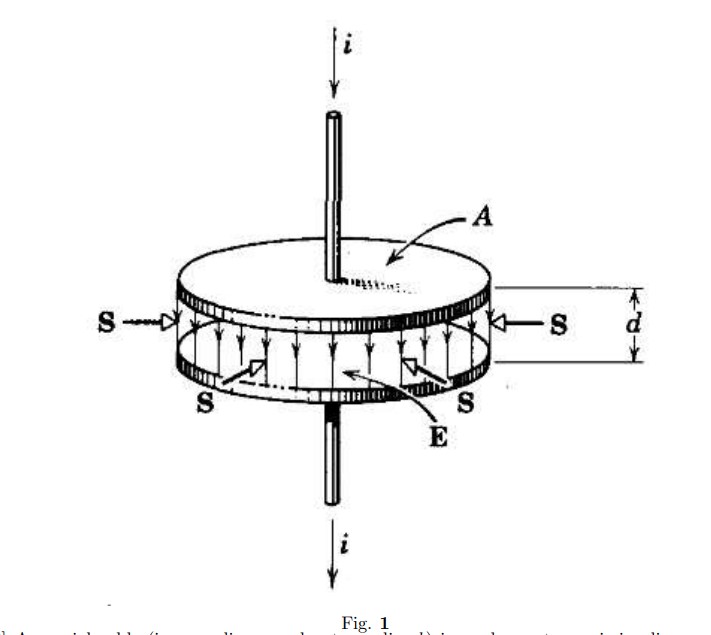
- Figure 1 shows a parallel-plate capacitor being charged,
- Show that the Poynting vector \(S\) points everywhere radially into the cylindrical volume.
- Show that the rate \(P\) at which energy flows into this volume, calculated by integrating the Poynting vector over the cylindrical boundary of this volume, is equal to the rate at which the stored electrostatic energy increases; that is, that \[\int \vec{S}\cdot\vec{dA} = A d \frac{1}{2}\frac{d}{dt}(\epsilon \vec{E}^2)\],where \(Ad\) is the volume of the capacitor and \(\frac{1}{2} \epsilon_0\vec{E}^2\) is the energy density for all points within that volume. This analysis shows that, according to the Poynting vector point of view, the energy stored in a capacitor does not enter it through the wires but through the space around the wires and the plates. \{Hint: To find \(S\) we must first find \(B\), which is the magnetic field setup by the displacement current during the charging process; Ignore fringing of the lines of \(E\).)\}
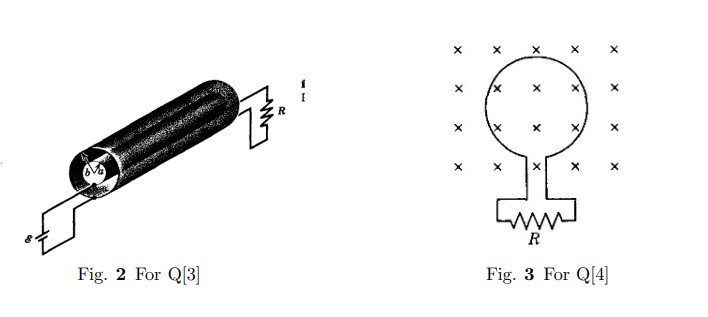
- A coaxial cable (inner radius \(a\) and outer radius \(b\)) is used as a transmission line between a battery $\epsilon$ and a resistor \(R\),
- [(a)] Calculate $\vec{E}, \vec{B}$ for $a < r < b$
- [(b)] Calculate Poynting vector S for $a< r < b.$
- [(c)] By suitably integrating the Poynting vector, Show that the total power flowing across the annular cross section $a<r<b$ is="" $\epsilon^{2}="" r$.="" this="" reasonable="" ?="" <="" li="">
- [(d)] Show that the direction of $\vec{S}$ is always away from the battery to resistor, no matter which way is the battery connected.
|

|
22-04-25 19:04:10 |
n |
|
|
[2019EM/HMW-05]Node id: 5367pageElectrodynamics Apr 14, 2018
Tutorial-V
- A cylindrical resistor of length \(\ell\), radius \(a\) and resistivity $\varrho$ is carrying a current \(i\).
- Show that the Poynting vector $\vec{S}$ at the surface of the resistor is everywhere directed to the normal to the curved surface.
- Show the rate $\rho$ at which energy flows into the resistor through its cylindrical surface, calculated by integrating the Poynting vector over this surface, is equal to the rate at which Joule heat is produced, i.e. \begin{equation*} \int\vec{S}\cdot\vec{dA}=i^2R \end{equation*}
- A long coaxial cable consists of two concentric conductors of radii \(a,b\) and length \(\ell\), see \Figref{Cable-Self-Ind}. The inner conductor is assumed to be a thin cylindrical shell. The conductors carry currents in opposite directions. Calculate self inductance of this cable in two ways:
- Using the definition of self inductance
- Using energy considerations.
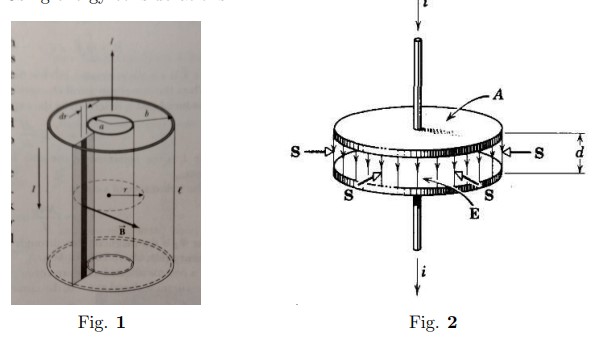
- \Figref{Capacitor} shows a parallel-plate capacitor being charged,
- Show that the Poynting vector \(S\) points everywhere radially into the cylindrical volume.
- Show that the rate \(P\) at which energy flows into this volume, calculated by integrating the Poynting vector over the cylindrical boundary of this volume, is equal to the rate at which the stored electrostatic energy increases; that is, that \[\int \vec{S}\cdot\vec{dA} = A d \frac{1}{2}\frac{d}{dt}(\epsilon \vec{E}^2)\],where \(Ad\) is the volume of the capacitor and \(\frac{1}{2} \epsilon_0\vec{E}^2\) is the energy density for all points within that volume. This analysis shows that, according to the Poynting vector point of view, the energy stored in a capacitor does not enter it through the wires but through the space around the wires and the plates. \{Hint: To find \(S\) we must first find \(B\), which is the magnetic field setup by the displacement current during the charging process; Ignore fringing of the lines of \(E\).)\}
- What happens when the current is taken to flow in the opposite direction?
- The Sun delvers about 1000 W/m\(^2\) of energy to earth's surface.
- Compute the power incident on a roof of dimension 5.0m\(\times\)8.0 m.
- Determine the radiation pressure and radiation force on the roof,assuming that the roof is a perfect absorber. \end{AlphaList1} You may assume that the Sun's rays are incident at 90\(^o\) on the roof. % Serway and Jerwett p315
|

|
22-04-25 19:04:57 |
n |
|
|
[2019EM/HMW-04]Node id: 5366pageElectrodynamics March 26, 2019
Tutorial-IV
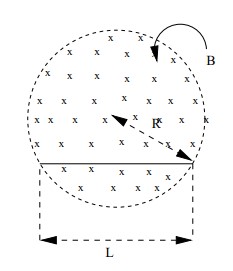
- A uniform magnetic field $\vec{B}$ fills a cylindrical volume of radius $R$ and a metal rod of length $L$ is placed in it as shown in the figure.If the magnitude $B$ is changing at the rate $\frac{dB}{dt}$ show that the emf that is produced by the changing magnetic field and that acts between the ends of the rod is given by $${\cal E} = \frac{dB}{dt}\frac{L}{2}\sqrt{R^2-\frac{L^2}{2}}$$
- Two identical coils each having radius $R$ and $n$- turns are kept parallel and with a distance $d$ between the two.
- Find an expression for the magnetic field at a point on the common axis of the coils and at a distance $x$ from the mid-point between the coils.
- Show that if the separation of the coils is equal to $R$, the first and the second derivatives of $B$ w.r.t. $x$ vanish at the mid point. This produces nearly constant magnetic field near the mid point, WHY?
- For $R=5.0$cm, $I=50$amp,and 300 turn coils, plot the magnetic field as a function of $x$ in the range $x=-5$cm to $x=5$cm.
.
- A wooden cylinder of mass $m=0.5$kg, radius $R=3$cm, length $\ell=10$cm, is placed on an inclined plane. It has 10 turns of wire wrapped around it longitudinally so that the plane of the wire contains the axis of the cylinder and is parallel to the inclined plane, see . Assuming no friction, what is the current that will prevent the cylinder from rolling down the inclined plane in presence of a uniform magnetic field of 0.5T?. Describe what happens if the block is a rectangular instead of a cylindrical one? What will be the current that will prevent the block from moving down the plane?
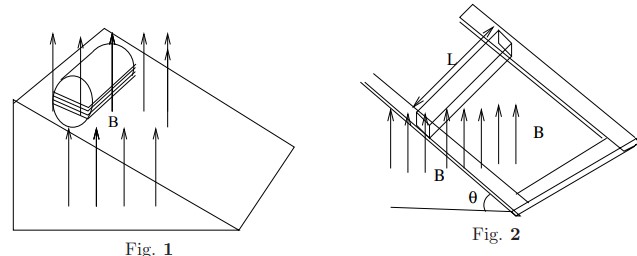
- A square wire of length $L$, mass $m$, and resistance $R$ slides without friction down parallel rails of negligible resistance, as in \Figref{em-fig-015}. The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and rails form a closed rectangular conducting loop. The plane of the rails makes an angle $\theta$ with the horizontal, and a uniform vertical magnetic field $\vec{B}$ exists in the region.
- Show that the wire acquires a steady state velocity of magnitude $$v= \frac{mgR\sin\theta}{B^2 L^2\cos^2\theta}$$
- Show that the above result is consistent with conservation of energy.
- What changes will be necessary in the above results, if the direction of magnetic field is reversed?
- A cylindrical shell of radius $R$, height $h$, and carrying a uniform surface charge density $\sigma$, rotates about its own axis with angular velocity $\omega$. Compute the magnetic field produced by the cylinder at a point on the axis
|

|
22-04-25 19:04:47 |
n |