Worked out example
For page specific messages
For page author info
Let a point P be at a distance r from the center of the sphere (radius=R) with charge density $\rho$
Consider a small thin shell of radius \(x\) and thickness \(dx\)
Volume of the shell = $4x^2\pi ax$
Charge contained in the shell =$4\pi x^2 \rho$

Problem
A solid sphere of radius \(R\) carries a charge density \(\rho(\vec{r})\). Show that the average of the electric field inside the sphere is \[\vec{E}= - \frac{1}{4\pi\epsilon_0} \frac{\vec{p}}{R^3},\] where \(\vec{p}\) is the total dipole moment of the sphere.
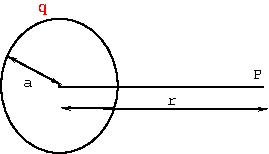
We will show that for a uniformly charged sphere, radius \(a\) and charge \(Q\),
the electric field is given by
\begin{equation}
\vec E = \begin{cases} 0 & \text{if } r<a\\
\frac{Q}{4\pi\epsilon_0 R^2 } & \text{if } r > a
\end{cases}
\end{equation} |
 |
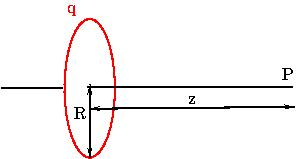
The electric field due to a charged ring, at a point, \(P\) on its axis, is computed using Coulomb's law. We will show that the electric field of uniformly charged ring, radius \(R\), at a point on the axis of the ring, is given by
\begin{equation}
\vec E = \frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \, \hat k.
\end{equation}
where \(q\) is the total charge and \(z\) is the distance if field point from the center of the ring. |
 |
A dipole is a system of two equal and opposite charges separated by a distance. Its electric field is computed and the field at large distances depends only on the dipole moment, defined as the product of the charge and separation between the charges.
While dipole is a system of two charges, the concept of dipole moment is defined and is useful for any system of charges with total zero charge.
Derive the Coulomb force due to a static charge on another static charge using the Maxwell stress tensor.
Two point charges \(Q\) and \(Q^\prime\) are located at positions given by \(\vec{a}, \vec{b}, (a\ne b) \). Find the conditions on \(Q, Q^\prime, a, b \) so that the potential on the surface of a sphere of radius \(R\) with center at the origin may be zero.
Note the result of this problem is used in solution for electric potential of a grounded conducting sphere in presence of a point charge by the method of images.
Pages
