Category:
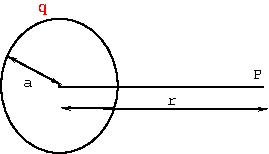
We will show that for a uniformly charged sphere, radius \(a\) and charge \(Q\),
| the electric field is given by \begin{equation} \vec E = \begin{cases} 0 & \text{if } r<a\\ \frac{Q}{4\pi\epsilon_0 R^2 } & \text{if } r > a \end{cases} \end{equation} |
 |
$\newcommand{\mHighLight}[2][]{#2}$
The surface charge density of a thin spherical shell is given to be uniform $\sigma$. We know that the field due to a ring for a point on the axis of the ring at a distance \(z\) is
\begin{eqnarray}
\vec{E}_z&=&\frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \label{eq13}
\end{eqnarray}
Now, we need to compute the electric field due to a thin spherical shell at a point \(P\).
The origin \(O\) of coordinate system is taken at the centre of the sphere. We divide the shell into thin strips of circular rings with planes perpendicular to the line \(OP\) as shown in Fig (a) below.
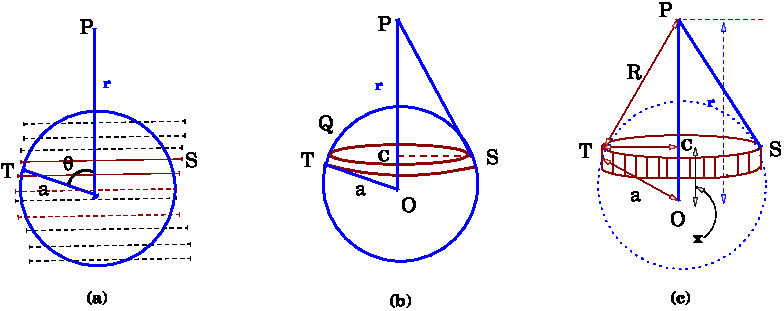
We consider a strip lying between \(x\) and \(x+dx\) as in Fig (b).
Then we have the expressions of different lengths as follows, see (c).
- Distance between the center of the shell and the strip= radius of the shell =\(OT\) = \(a\).
- Distance of the center, \(O\), of the shell from the field point \(P\) = \(OP\)= \(r\).
- Distance of the center of the shell, \(O\), from the center, \(C\), of the strip = \(OC\) =\(x =a \cos\theta\).
- The radius of the strip\( = CT = r_0 = a \sin \theta\).
Consider a ring shaped strip, as above, lying between \(x\) and \(x+dx\). The corresponding range of angles $\theta$ and $\theta+d\theta$ is shown in the figure. This slice is a ring of radius $r_0$ and is at a distance \(x\) from the centre. Then
\begin{equation} x=a\cos\theta,\qquad r_0=a\sin\theta, \qquad z=r-x=r-a\cos\theta. \end{equation}
where \(a\) denotes the radius of the shell and \(z\) is the distance of the slice from the point \(P\).
The ring can be regarded as a closed strip of length \(2\pi r_0\) and width \(ad\theta\). Therefore, its area is \(dS=2\pi r_0 a d\theta\) and the charge on the strip will be \[ dq = \sigma dS = \sigma (2\pi r_0 a d\theta)\]
We will express the charge in terms of the radius \(a\) and the total charge \(Q\) on the sphere. Noting \(Q=\sigma (4\pi a^2)\), we get
\begin{eqnarray}
\nonumber dq&=&(ad\theta)(2\pi a \sin \theta) \sigma
=\Big(\frac{Q}{4\pi a^2}\Big) a^2 (2\pi\sin \theta\, d\theta) \\
\text{or } dq&=&\frac{Q}{2}\sin \theta\, d\theta \label{eq15}
\end{eqnarray}
Using the result for the field of a ring we get electric field of the ring as \begin{equation} dE = \frac{dq}{4\pi \epsilon_0}\frac{1}{R^2} \label{EQ22} \end{equation} where is the distance \(PT\) of the point \(P\) from the ring. We need to express \(R\) in terms of \(a\) and \(\theta\). From (c) we note that
\begin{eqnarray}
R^2 &=& CT^2+ CP^2\\
&=& r_0^2 + (r-x)^2\\
&=&a^2 \sin^2\theta + (r-a \cos\theta)^2\\
&=& r^2+a^2 -2ar \cos\theta.
\end{eqnarray}
Using this expression for \(R\) in \eqref{EQ22} and integrating over \(\theta\) we get\begin{eqnarray}
E&=&\frac{1}{4\pi\epsilon_0}\int_0^{\pi}\frac{Q\sin \theta
d\theta(r-a\cos\theta)}{2(r^2+a^2-2ar\cos\theta)^{3/2}}\\
\nonumber&=&\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}\frac{
(r-at)dt}{2(r^2+a^2-2art)^{3/2}}\qquad \mHighLight[LightCyan]{t=\cos\theta}\\
\nonumber&=&\frac{1}{2}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}\frac{1}{r}\frac{
r^2-atr}{(r^2+a^2-2art)^{3/2}}dt\\
\nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}
\frac{\mHighLight[lime]{$r^2$}+\frac{1}{
2}(r^2+a^2-2atr)-\mHighLight[lime]{\frac{1}{2}(r^2+a^2)}}{(r^2+a^2-2art)^{3/2}}dt\\
\nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}\int_{-1}^{1}
\Big[\frac{1}{2}\frac{\mHighLight[lime]{
(r^2-a^2)}}{(r^2+a^2-2art)^{3/2}}dt+\frac{1}{2}
\frac{(dt)}{(r^2+a^2-2art)^{1/2}}\Big]\\
\nonumber&=&\frac{1}{2r}\frac{Q}{4\pi\epsilon_0}\Big[\frac{1}{2}\frac{(r^2-a^2)}{
ar(r^2+a^2-2art)^{1/2}} - \frac{1}{2ar}(r^2+a^2-2art)^{1/2}\Big]_{-1}^{+1}
\label{eq16}
\end{eqnarray} Before proceeding further, it is important to note that
\[\sqrt{r^2+a^2-2ar}=|a-r|=
\begin{cases}
r-a, & \text{ if } r>a \\
a-r, & \text{ if } r<a.
\end{cases}\]
Case $r>a$:
\begin{eqnarray}
\nonumber{E}&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0r}\left[\left\{\frac{(r^2-a^2)}{r-a}
- (r-a)\right\}- \left\{\frac{r^2-a^2}{r+a} - (r+a)\right\}\right]\\
\nonumber&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0r}\big[\{(r+a) - (r-a)\}- \{(r-a)-
(r+a)\}\big]\\
&=&\frac{Q}{4\pi\epsilon_0r^2} \label{eq17}
\end{eqnarray}
Case $r<a$:
\begin{eqnarray}
\nonumber {E}&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0r}\Big[\Big\{\frac{(r^2-a^2)}{a-r}
- (a-r)\Big\}- \Big\{\frac{r^2-a^2}{r+a} - (r+a)\Big\}\Big]\\
\nonumber&=&\frac{1}{2ar}\frac{Q}{8\pi\epsilon_0r}\big[\big\{-(r+a) - (a-r)\big\}- \big\{(r-a)-
(r+a)\big\}\big]\\
&=&0. \label{eq18}
\end{eqnarray}






 ||Message]
||Message]
