Category:
A dipole is a system of two equal and opposite charges separated by a distance. Its electric field is computed and the field at large distances depends only on the dipole moment, defined as the product of the charge and separation between the charges.
While dipole is a system of two charges, the concept of dipole moment is defined and is useful for any system of charges with total zero charge.
A dipole is a system of equal and opposite charges. We will compute the electric field at a points \(P\) and \(Q\) due to charges \(-q, q\), separated by distance \(d\), and located at points \(A,B\) respectively, as shown in the \Figref{dipole-1}. We will consider the limit when the field points are a much larger than the distance between the charges, {\it i.e.}, \(r>>d\).
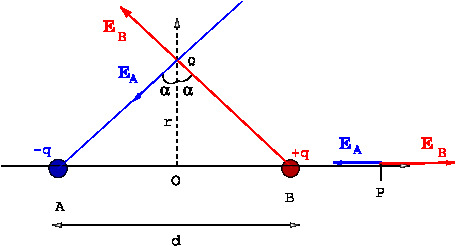
Electric field at a point \(P\) Let \(OP=r\) as in the figure.
\begin{eqnarray}
\nonumber{E}_P&=&\frac{1}{4\pi\epsilon_0}\Big[\frac{q}{(r-d/2)^2}-\frac{q}{
(r+d/2)^2}\Big]\\
\nonumber&=&\frac{q}{4\pi\epsilon_0}\Big[\frac{(r+d/2)^2-(r-d/2)^2}{
(r-d/2)^2(r+d/2)^2}\Big]\\
&=&\frac{q}{4\pi\epsilon_0}\frac{2rd}{(r^2-d^2/4)^2} \label{eq19}.
\end{eqnarray}
Electric field at the point \(Q\)
At the point \(Q\) the vertical components of the fields \(\vec E_A, \vec E_B\) cancel and the horizontal components add up. Therefore, the electric field at \(Q\) is along the horizontal direction and its magnitude is given by
\begin{eqnarray}
{E}_Q=E_A\sin \alpha + E_B \sin \alpha = 2E_A \sin \alpha.\qquad \text{ where } \sin\alpha = \frac{\text{OA}}{\text{QA}} \label{eq21}.
\end{eqnarray}
because the magnitude \(E_A, E_B\) of the fields due to the two charges at \(Q\) are equal. Let \(r\) denote the distance of the point \(Q\) from the origin, \(r=OQ\), then
\begin{eqnarray}
E_A&=&E_B=\frac{q}{4\pi\epsilon_0}\frac{1}{(r^2+d^2/4)}\\ \label{eq22}
\nonumber {E}_Q&=&\frac{2q}{4\pi\epsilon_0}\frac{1}{(r^2+d^2/4)}\frac{d/2}{
(r^2+d^2/4)^{1/2}}\\
&=&\frac{qd}{4\pi\epsilon_0 (r^2+d^2/4)^{3/2}} \label{eq23}
\end{eqnarray}
Defining $p=qd$ as the dipole moment of the charge system,
\begin{eqnarray}
{E}_P&=&\frac{2p r}{4\pi\epsilon_0 (r^2-d^2/4)^2}, \qquad
{E}_Q =\frac{p}{4\pi\epsilon_0 (r^2+d^2/4)^{3/2}}. \label{eq26}
\end{eqnarray}
And for large \(r\), $r>>d$
\begin{eqnarray}
\qquad
{E}_P&\approx&\frac{2p}{4\pi\epsilon_0 r^3},
\qquad
{E}_Q \approx\frac{p}{4\pi\epsilon_0 r^3}. \label{eq25}
\end{eqnarray}
The above expressions give the leading contribution of the charge system for large distances. How much large is large \(r\)? \(r\) is taken large compared to the separation \(d\).
While a dipole is a system of two equal and opposite charges, the concept of dipole moment generalizes to the system of several charges and also to system with continuous charge distribution. The dipole moment for several point charges is defined by
\begin{equation} \vec p = \sum_k q_k \vec r_k. \end{equation}
It is easy to check that the for \(Q\ne0\), the dipole moment changes if the system is translated. On the other hand if \(Q=0\), the dipole moment is invariant under translations. Therefore it is a property of the system when the total charge is zero.






 ||Message]
||Message]
