Category:
The electric field due to a charged ring, at a point, \(P\) on its axis, is computed using Coulomb's law. We will show that the electric field of uniformly charged ring, radius \(R\), at a point on the axis of the ring, is given by
| \begin{equation} \vec E = \frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \, \hat k. \end{equation} where \(q\) is the total charge and \(z\) is the distance if field point from the center of the ring. |
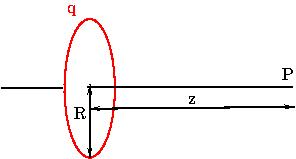 |
We choose the origin of the coordinate system at the centre of the ring and work with plane polar coordinates \(r,\phi\). Divide the ring into small elements. One such element, lying in range \(\phi\) and \(\phi+d\phi\) is shown in \Figref{Field-Ring}(a) and (b). The radius of the loop is $ r_0$. The electric field is to be calculated at a point \(P\) on the \(Z\)- axis which is taken to coincide with the axis of the loop.
The charge on the line element is \(AB\) is \(dq=\lambda r_0 d\phi\). and the electric field points along \(AP\) and has magnitude \(dE\), where \begin{equation} dE = \frac{dq}{4\pi\epsilon_0 R^2} \end{equation} The horizontal component of the field, at the point \(P\), due to the ring vanishes. This can be seen by considering contributions from two diametrically opposite line elements as indicated in
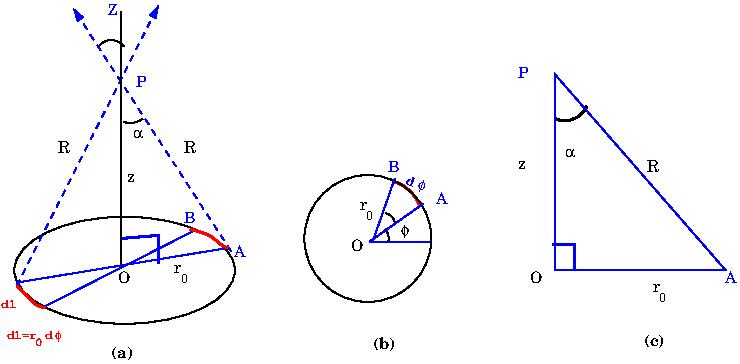
We, therefore, need to compute only the \(z\)-component of the electric field. The \(z\)- component of the field due to the line element \(AB\) is seen to be \begin{equation} dE_z = dE \cos \alpha =\frac{\lambda dl}{4\pi\epsilon_0 R^2}(\cos\alpha) , \end{equation} and the total field can be written as \begin{eqnarray} {E}_z&=&\int\frac{\lambda dl}{4\pi\epsilon_0 R^2}(\cos\alpha) \label{eq7}, \end{eqnarray} From the figure we have $dl=r_0d\phi$, $ \cos\alpha=\frac{z}{R}$ and $R=\sqrt{z^2+r_0^2}$. Therefore
\begin{eqnarray} \nonumber{E}_z&=&\int\frac{\lambda r_0 d\phi}{4\pi\epsilon_0 (z^2+r_0^2)}(cos\alpha)=\frac{\lambda z r_0}{4\pi\epsilon_0 (z^2+r_0^2)^{3/2}}\int d\phi\\ \nonumber&=&\frac{\lambda z r_0}{4\pi\epsilon_0 (z^2+r_0^2)^{3/2}}(2\pi) \\ E_z&=&\frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \label{eq8} \end{eqnarray} where $q=2\pi r_0\lambda$ is the total charge on the ring. Thus the final answer for the electric field is given by \begin{equation} \vec E = \frac{qz}{4\pi\epsilon_0(z^2+r_0^2)^{3/2}} \, \hat k. \end{equation} For large \(z\), the field becomes \begin{eqnarray} {E}_z\approx \frac{q}{4\pi\epsilon_0z^2} \label{eq9}. \end{eqnarray}
This is understandable because the ring would appear to be point like and the entire charge \(q\) on the ring appears to concentrated at a single point.
One important point, not to be missed, is that one must remember that 'large', or 'small', always means compared to some quantity. In the present case large \(z\) means \eqref{eq9} holds for \(z>>r_0\).






 ||Message]
||Message]
