|
|
[2019EM/Final]Node id: 5349pageTIME :3hrs ELECTRODYNAMICS MM:100
End Semester Examination
ATTEMPT ANY FIVE QUESTIONS.
- Find the potential due to a sphere carrying a uniform polarization \(\vec{P}\). The centre of the sphere is at the origin and radius of the sphere is \(R\). What is the electric field at a point (i) inside the sphere (ii) outside the sphere?
- Give an example of a charge configuration such that its dipole moment is zero and quadrupole moment depends on the choice of origin.
- An alpha particle travels in a circular path of radius $0.45$m in a magnetic field with $B=1.2$w/m$^2$. Calculate (i) its speed (ii) its period of revolution, and (iii) its kinetic energy.Mass of alpha particle = \(6.64424. 10^{-27}\)kg \(\approx 4\times M_p= 4\times938.27\) MeV.
- A circular coil is formed from a wire of length $L$ with $n$ turns. The coil carries a current $I$ and is placed in an external uniform magnetic field $B$. Show that maximum torque developed is $\displaystyle\frac{IBL^2}{4n\pi}$.
- Give examples of at least six results/concepts that require modifications in time varying situation. [4+5+5+6]
- Derive an expression for electrostatic energy of a charge distribution and hence show that electric field carries energy density \(\frac{\epsilon_0}{2}|\vec{E}|^2\).
- A conducting spherical shell carries a charge \(Q\), compute its electrostatic energy and hence obtain an expression for the capacitance of the shell.\hfill[10+10]
- A rod of mass $m$ and length $\ell$ and resistance $R$ starts from rest and slides on two parallel rails of zero resistance as shown in figure 1. A uniform magnetic field fill the area and is perpendicular and out of the plane of the paper. A battery of of voltage $V$ is connected as shown in the figure 1.
- Argue that the net EMF in the loop is $V = Bv\ell$ when the rod has speed $v$.
- Write down $F = m\big(\dfrac{dv}{dt}\big)$ and integrate it so show that \begin{equation*}\label{EQ01} v(t) =\frac{V}{B\ell}\Big(1- \exp\Big(- \frac{B^2\ell^2 t}{mR}\Big)\Big). \end{equation*} Hint: Find the limiting speed and separate that out from the total $v$.
- What happens when the direction of magnetic field is reversed? [8+8+4]

- Show that, in absence of charges and currents, the electric and magnetic fields obey wave equation.
- State and prove important properties of plane wave solutions.
- Obtain an expression for energy density and intensity of plane waves. [6+8+6]
- An infinite rectangular hollow pipe is bounded by the planes \(x=\pm a,y=0, y=b\). The pipe extends to infinity in positive as well as negative \(Z\)- directions. The sides \(y=0, x=\pm a\) are grounded and the the side \(y=b\) is held at constant potential \(\phi_0\). Show that the potential inside the pipe is \begin{equation*} \phi(x,y) = \phi_0\Big\{\frac{y}{b} +\frac{2}{\pi} \sum_{n=1}^\infty\frac{(-1)^n}{n} \frac{\cosh (n\pi x/b)}{\cosh(n\pi a/b)} \sin (n\pi y /b) \Big\} \end{equation*}
|

|
22-04-03 11:04:05 |
n |
|
|
[2019EM/MidSem-1]Node id: 5350page Mid Semester Examination∗
B.Sc. IInd Sem MM: 30
- A circular disk of radius \(R\) carries a surface charge density \(\sigma=kr\). Find the potential at a point on the axis of the disk and distance \(d\) from the center of the disk.
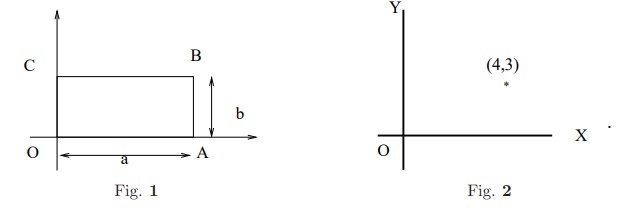
- Two grounded infinite conducting planes are kept along the \(XZ\) and \(YZ\) planes, see Fig.2. A charge \(Q\) is placed at (4,3) find the force acting on the charge \(Q\).
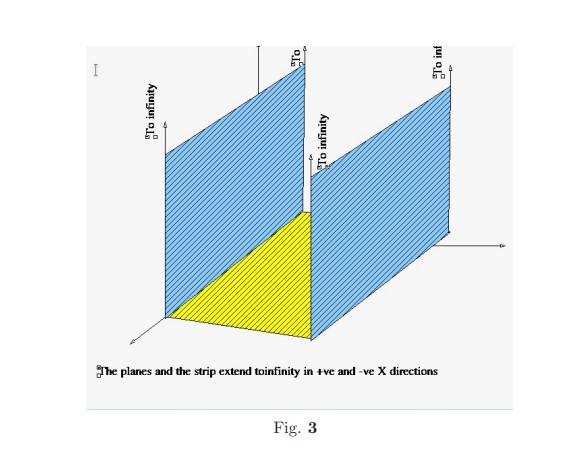
- Solve the boundary value problem in volume \(V\) bounded by semi-infnite planes (i) Plane 1:\(XZ\) plane extending to infinity in positive \(z\) and both positive and negative \(x\) directions.(ii)Plane 2: Another plane parallel to Plane 1 obtained by translating it to \(y=L\)(iii)Infinite strip: A strip lying in \(XY\) plane between \(0\le y \le L\). The boundary conditions required to be satisfied are \begin{equation} \phi(x,y,z)= \begin{cases} 0 & \text{for } y=0 \text{ and all } x, z\\ 0 &\text{for } y=L \text{ and all } x, z\\ 0 & \text{ as } z \to \infty \\ \cos(3\pi y/L) \sin(5\pi y/L) & \text{ for } z=0 \text{ and } 0\le y \le L \end{cases} \end{equation}
|

|
22-04-03 11:04:09 |
n |
|
|
[2019CM/Final-Part-B]Node id: 5339page$\newcommand{\Lsc}{\mathscr L}$
Classical Mechanics July 4, 2009
End Semester Examination::PART-B
Instruction:-Attempt any four questions.
- Consider a particle of mass $m$ moving in two dimensions in a potential The equation of motion for small oscillations are given to be [4+4+4] \begin{eqnarray} m\ddot{x} =k \big( 5x + y \big)\\ m\ddot{y} =k \big( x + 5 y \big)\nonumber \end{eqnarray}
- Find the normal frequencies of vibration of normal modes.
- Obtain expressions for \(x,y\) in terms of normal coordinates.
- Write the Lagrangian \[{\Lsc} = \frac{m}{2}(\dot{x}^2+m\dot{y}^2) - \frac{k}{2}\big(5x^2+2xy +5y^2\big)\] in terms of normal coordinates and verify that it takes the form \[{\Lsc} = \frac{1}{2}(\dot{Q}_1^2+\dot{Q}_2^2) - \frac{1}{2}(\omega_1^2Q_1^2+\omega_2^2Q_2^2)\]
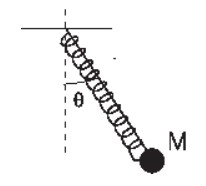
- Consider pendulum with a spring shown in figure. It oscillates in vertical plane like any simple pendulum.
- What is number of degrees of freedom? Which generalized coordinates will you use?[2+2+8]
- Write the Lagrangian for the system.
- A missile is fired from the origin with initial velocity \(u\) and at an angle \(\alpha\) with horizontal. [3+3+3+3]
- Write the Lagrangian for the missile.
- Is there a cyclic coordinate? Which one? What is the conserved quantity associated with it?
- Is there any other conserved quantity?
- Using conserved quantities you have found, briefly indicate how a full solution can be obtained.
-
- Show that [3+3+6] \begin{equation*} Q=-p ,\qquad P=q + Ap^2 \end{equation*} (where A is any constant) is a canonical transformation,
- [(i)] by evaluating \([Q,P]_{q,p}\)
- [(ii)] by expressing \(pdq-PdQ\) as an exact differential \(dF(q,Q)\). Hence find the type one generating function of the transformation. To do this, you must first use the transformation to express \(p,P\) in terms of \(q,Q\).
- Use the relation \(F_2=F_1+PQ\) to find the type 2 generating function \(F_2(q,P)\),and check your result by showing that \(F_2\) indeed generates the transformation.
- Consider the motion in a spherically symmetric potential $$ V(r) = - V_0 \left( {3 R\over r } + {R^3\over r^3} \right)$$ If orbital angular momentum of the particle is given by $l^2 = 10 m V_0 R^2$, and answer the following questions.
- Plot the effective potential as a function of $r$ [3]
- What should be the energy of the particle so that it may move in a circular orbit? How many circular orbits are possible? Find the radius of the stable orbit. [3+3+3]
|

|
22-04-03 11:04:23 |
n |
|
|
[2019CM/QUIZ-02]Node id: 5341pageClassical Mechanics June 17, 2019
Quiz-II
- For a system with coordinates \(q_k\) and canonical momenta \(p_k\), compute the Poisson brackets \begin{equation} \{q_k, F(q,p)\}_\text{PB}; \qquad \qquad\{p_k, G(q,p)\}_\text{PB} \end{equation}
- Set up Lagrangian for a coupled pendulum shown in figure below. Assume that the system while oscillating remains in a vertical plane.
|

|
22-04-03 11:04:30 |
n |
|
|
Physics of Information 2022 --- A Course being offered Currently at CMI --- H.S. ManiNode id: 5229collectionPhysics of Information
A Course being Offered Currently at Chennai Mathematical Institute
- Lecture Notes
- Home Work and Solutions
- Test and Examination Papers
- Suggested for Further Study
- Video Recording Links
- Lecture 1 -- Jan 25, 2022
- Review of Laws of Thermodynamics; Concept of EntropyCarnot Engine;Maxwell's Demon
- Lecture 2 -- Jan 28, 2022
- Maxwell's Demon 2;Work of Landauer and Bennet
- Lecture 3 -- Feb 1, 2022
- Landauer Bennet argument; erasure of information costs energyInformation and Entropy; Shannon Entropy; Joint Entropy;Connection with Equilibrium Statistical Mechanics
- Lecture 4 -- Feb 3, 2022
- Erasure of Information; Different Protocols;Work Done in A Measurement; Classical Information Theory;Joint Entropy; Conditional Entropy;Mutual Information;An Example
- Lecture 5 -- Feb 8, 2022
- Quantum Information Theory Joint Entropy; Conditional Entropy; Mutual InformationMeasurement in Quantum Mechanics; Projective Measurement;Positive Operator Valued Measurement; Relative Entropy
- Lecture 6 --- Feb 10, 2022
- Measurement; Projective Measurement; Positive Operator Valued Measurement
- Lecture 7 --- Feb 15, 2022
- Change in entropy in a projective measurement; Purification;Concave property of von Neumann entropy
- Lecture 8 --- Feb 17, 2022
- Lecture 9 --- Feb 22, 2022
- Lecture 10 Feb 24, 2022
- Lecture 11, Mar 1, 2022
- Lecture 12 Mar 4, 2022
- Lecture 13 Mar 8, 2022
- Lecture 14. Mar 15, 2022
- Lecture 15 March 24, 2022
Books recommended
- Michael A.Nielsen and Issac L. Chuang, "Quantum Information and Quantum Computing", Cambridge University Press, Cambridge (2000)
- Mark M. Wilde,"Quantum Information Theory", Cambridge University Press Cambridge (2013)
- Thomas M. Cover and Joy A. Thomas, "Elements of Information Theory" Wiley-Interscience 2nt Edn (2006)
- Harvey S Leff and Andrew F. Rex (ed.) "Maxwell's Demon2-- Entropy, Classical and Quantum Information Computing", Institute of Physics Publishers, Bristol (2003)
|

|
22-04-03 08:04:08 |
n |
|
|
Curated video contentNode id: 3548video_page |

|
22-04-02 23:04:50 |
n |
|
|
Normal Modes of Coupled PendulumNode id: 4172video_page |

|
22-04-02 23:04:35 |
n |
|
|
Solved Example --- Thermodynamics@CMI 2021 by H. S. Mani Node id: 4815video_pageProfessor Mani discusses an example of a solid in contact with a reservoir at a lower temperature. After the system has reached equilibrium the entropy of the system increases. This is demonstrated by an explicit calculation. Several important remarks are made. In particular how the equilibrium can be achieved by a reversible quasi static process, in which case there will be no change in entropy.
|

|
22-04-02 23:04:00 |
n |
|
|
Normal Modes of Coupled Pendulum-IINode id: 4171video_page |

|
22-04-02 23:04:27 |
n |
|
|
Normal Modes of a Double Pendulum-INode id: 4174video_page |

|
22-04-02 23:04:03 |
n |
|
|
Warehouse --- Collection -IV Contributed Study MaterialNode id: 5347collection |

|
22-04-02 15:04:03 |
n |
|
|
WAREHOUSE ---- Collection I Short Examples [All Areas]Node id: 4806collectionTHE AVAILABLE RESOURCES ARE BEING REORGANIZED
All links may not be available at this time
Warehouse-I --- Short Examples [ALL AREAS]
CHOOSE A SUBJECT AREA
Mathematical Physics Resources
- Complex Variables
- Finite Dimensional Vector Spaces
- Group Theory
- Matrices
- Ordinary Differential Equations
- Partial Differential Equations
- Orthogonal Polynomials
- Fourier Series, Fourier Transform
- Set Theory
Physics Resources
- Classical-Mechanics
- Electromagnetic Theory
- Elementary Particle Physics
- General Relativity
- Lie Groups and Lie Algebras
- Newtonian Mechanics
- Nuclear Physics
- Optics
- Quantum Information and Quantum Computation-Home
- Quantum Field Theory
- Quantum Mechanics
- Statistical Mechanics
- Thermodynamics
- Waves and Oscillations
|

|
22-04-02 15:04:34 |
n |
|
|
[2019CM/TEST-01]Node id: 5343pageClassical Mechanics July 3, 2019
$\newcommand{\Lsc}{\mathscr L}$
Test-I
- For a system the Hamiltonian is given to be \begin{equation*} H(q,p) = \frac{p^\beta}{\beta} + V(q) \end{equation*}
- Obtain Hamilton's equations of motion.\hfill[3]
- Show that the Lagrangian of the system is given by [4] \[L = \frac{q^\alpha}{\alpha} -V(q)\] where \(\alpha\) is given by \[ \frac{1}{\alpha} + \frac{1}{\beta}=1\]
- Consider a particle of mass $m$ moving in two dimensions in a potential The equation of motion for small oscillations are given to be \begin{eqnarray} m\ddot{x} = \frac{1}{2}\big( 3x + y \big)\\ m\ddot{y} = \frac{1}{2}\big(x + 3 y \big)\\ \end{eqnarray} [5+5+5]
- Find the normal frequencies of vibration in (b).
- Obtain expressions for \(x,y\) in terms of normal coordinates.
- Write the Lagrangian in terms of normal coordinates and verify that it takes the form \[{\Lsc} = \frac{1}{2}(\omega_1^2\dot{Q}_1^2+\omega_2^2\dot{Q}_2^2) - \frac{1}{2}(Q_1^2+Q_2^2)\]
- Find a differential equation for \(f(P)\) so that the transformation[3+2+3] \begin{equation*} q=\frac{f(P)}{m\omega} \sin Q, \quad p= f(P) \cos Q \end{equation*} may be a canonical transformation.
- Solve the differential equation you get subject to condition \(f(0)=0\) and show that \[ f= \sqrt{2m\omega P}\]
- Obtain the type 1 generator for this transformation.
|

|
22-04-01 14:04:43 |
n |
|
|
[2019CM/QUIZ-03]Node id: 5342pageClassical Mechanics June 24, 2019
Quiz-III
- Define spherically symmetric potential. [4]
- Plot effective potential for isotropic oscillator potential \(V(r)=\frac{1}{2}m \omega^2r^2\). Find the radius of circular orbit(s). [6]
- Under a rotation of coordinate axes about \(\hat{n}=\frac{1}{\surd 3}(1,1,1)\) by an angle \(\pi/3\) what will be the vectors representing the new axes?
.
|

|
22-04-01 13:04:09 |
n |
|
|
[Solved-ODE_02007] Frobenius Method --- Case IVNode id: 1807page |

|
22-04-01 12:04:59 |
n |
|
|
[Solved/ODE-02004] Frobenius Method --- Case IVNode id: 1804page |

|
22-04-01 12:04:39 |
n |
|
|
[Solved/ODE-02002] Frobenius Method --- Case-IIINode id: 1802page |

|
22-04-01 11:04:51 |
n |
|
|
Contributed Problem Sets Node id: 5337collection
- 2019Classical Mechanics
- 2019CM/HMW-01
- 2019CM/HMW-02
- 2019CM/HMW-03
- 2019CM/HMW-04
- 2019CM/HMW-05
- 2019CM/HMW-07
- 2019CM/HMW-08
- 2019CM/QUIZ-01
- 2019CM/QUIZ-02
- 2019CM/QUIZ-03
- 2019CM/QUIZ-04
- 2019CM/TEST-01
- 2019CM/EXM-01
- 2018 Classical Mechanics
|

|
22-04-01 07:04:59 |
n |
|
|
LSN/QFT-04001:: Second Quantization of Schrodinger FieldNode id: 3881draftnode |

|
22-04-01 05:04:10 |
n |
|
|
[NOTES/QFT-04006] Normal Products and Matrix Elements Node id: 3889page |

|
22-03-31 12:03:05 |
n |