|
|
[NOTES/QCQI-03002] Density MatrixNode id: 5027page |
|
22-04-07 13:04:50 |
n |
|
|
[NOTES/QCQI-03003] Density Matrix of Mixed State Node id: 5028page$\newcommand{\average}[2]{\langle#1|#2|#1\rangle}$ |
|
22-04-07 13:04:02 |
y |
|
|
[NOTES/QCQI-01005] Bloch Sphere Node id: 5022page |
|
22-04-07 13:04:01 |
y |
|
|
[NOTES/QCQI-01002] Two Level System as a QubitNode id: 5019page |
|
22-04-07 13:04:27 |
n |
|
|
[NOTES/QCQI-01001] Binary Number RepresentationNode id: 5016page |
|
22-04-07 13:04:29 |
n |
|
|
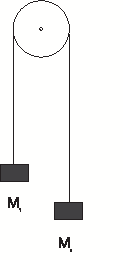
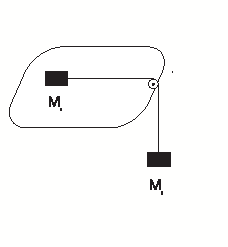
[QUE/CM-02004]Node id: 2536page
Set up the Lagrangian for two masses \(M_1,M_2\) tied to ends of an inextensible string passing over a pulley and placed as follows.
- Both masses are hanging on the two sides of the pulley.( Fig 1(a)).
- One of the masses \(M_1\) lies on a frictionless horizontal table and the other mass \(M_2\) hangs vertically as in Fig 1(b).
- One of the masses \(M_1\) lies on a frictionless inclined plane and the other mass \(M_2\) hangs vertically as in Fig 1(c).
|
 |
 |
 |
| Fig1(a) |
Fig1(b) |
Fig1(c) |
|
|
22-04-06 17:04:31 |
n |
|
|
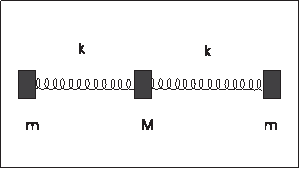
[QUE/CM-02005]Node id: 2537page
| Set up the Lagrangian for the system of three masses tied two the ends of two light springs as shown in figure below. Assume that the molecule vibrates only along the line joining the atoms. |
. |
|
|
22-04-06 17:04:53 |
n |
|
|
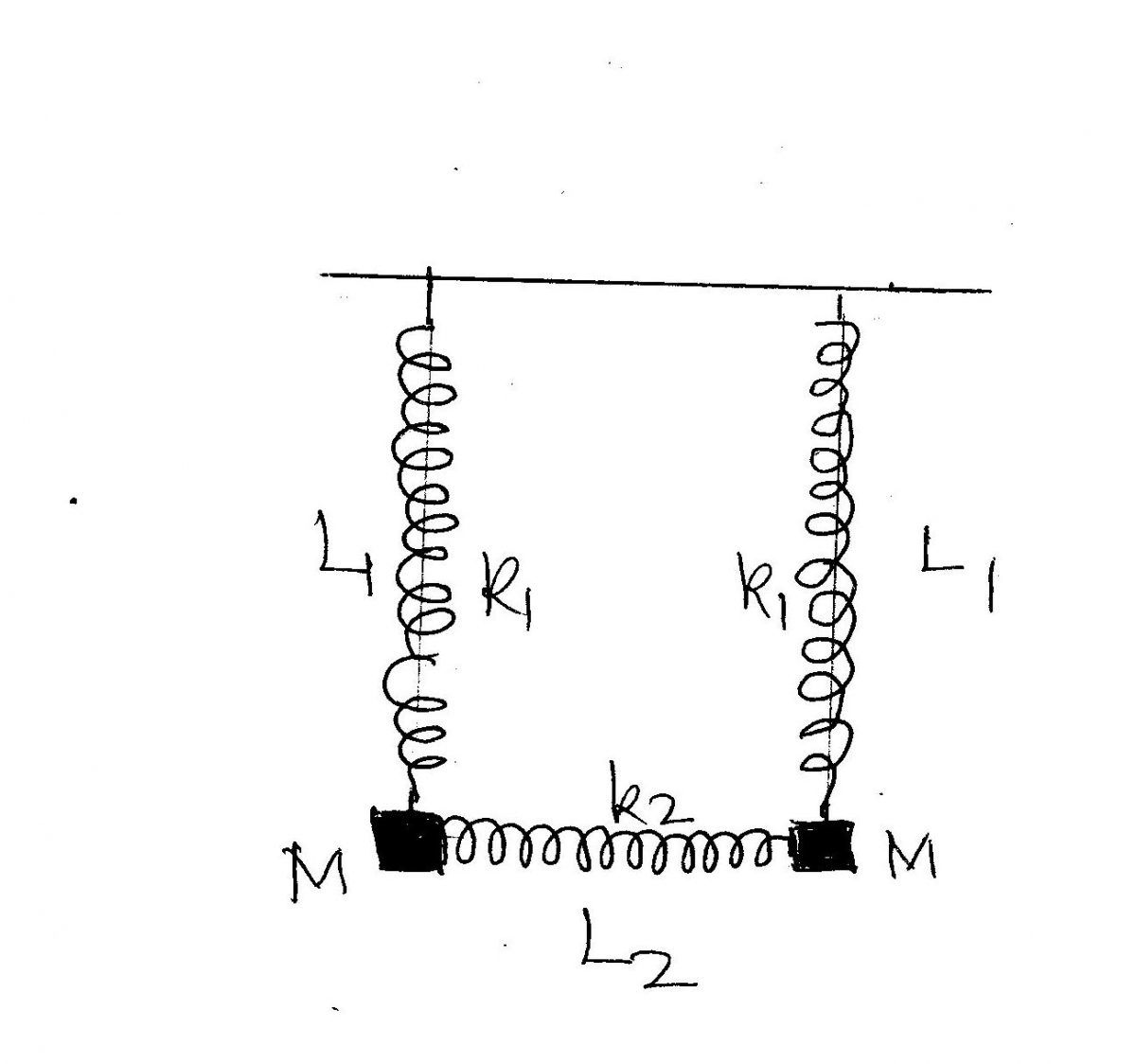
[QUE/CM-02006]Node id: 2538page
| Two equal masses, $M$, are tied to two springs hanging vertically and a third spring connects them as shown in the figures. All the three springs have natural lengths \(L\). Also in equilibrium the separation of the masses is also \(L\). Assume that the two masses are constrained to move arbitrily in the vertical plane only. What is the number o degrees of freedom of the system. Write the Lagrangian of the system ignoring the masses of the spring. |
 |
|
|
22-04-06 17:04:36 |
n |
|
|
[QUE/CM-02008]Node id: 2539page
A mass $M$ is tied to two springs, spring constants \(k_1,k_2\), and lies on a smooth horizontal table as shown in figure. The free ends of the springs are held fixed at points separated by a distance $(L_1+L_2)$, where $L_1,L_2$ are the natural lengths of the springs.
|
F |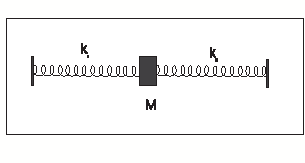
Write the Lagrangian for the following cases:
(a) The body is constrained to move only in a line along the springs.
(b) The body moves in a straight line only perpendicular to the springs.
(c) The body can move in any direction on the table. |
|
|
22-04-06 16:04:53 |
n |
|
|
[QUE/QM-08001]Node id: 2753pageThe potential energy of two protons in hydrogen molecule ion in a model is given below
\begin{eqnarray}
V(x) &=& |E_1| f(x) \\
f(x) &=& - 1 + \frac{2}{x}\left[ \frac{(1-(2/3)x^2) e^{-x} + (1+x) e^{-2x}}
{1+(1+x+x^2/3) e^{-x} }\right], \qquad x=R/a
\end{eqnarray}
$E_1= 13.6 \text{ eV}$ is the ground state energy of H atom and $a$ is the Bohr radius $\hbar^2/me^2$. The graph of this function $f(x)$ is reproduced below. Find numerical values of the bond length in ${A^o}$, the zero point energy and spacing of vibrational spectrum, both energies in electron volts.
NoteThe expression for $V(x)$ is taken from an approximate variational calculation of energy of the H molecule ion in Born Oppenheimer approximation.
|
|
22-04-06 16:04:34 |
n |
|
|
[QUE/QM-13002]Node id: 2768page
- Find the energy eigen-functions for $E < V_0$. Verify that the energy eigenvalues are non-degenerate and continuous in this case.
- Verify that the energy eigenvalues are doubly degenerate for $E > V_0$. Find two linearly independent energy eigenfunctions $u_1$ and $u_2$ for energy $E$ such that the most general energy eigenfunctions is a linear combination of the two solutions $u_1$ and $u_2$.
|
|
22-04-06 16:04:46 |
n |
|
|
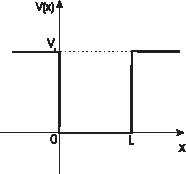
[QUE/QM-07002]Node id: 2815page
Consider a particle in one dimensional square well potential
\begin{equation}
V(x) = \left\{ \begin{array}{ll}
0 & 0 \le x \le L \\
V_0 & \mbox{otherwise}
\end{array} \right.
\end{equation}
For a bound state we should have average energy less than V_0$. $$ \langle E\rangle =\langle T\rangle + \langle V\rangle < V_0 $$
where $\langle T\rangle$ and $\langle V\rangle$ are the averages of the kinetic and the potential energies, respectively. If the article is to be confined to a region of size $L$, use the uncertainty principle to get a rough estimate of average kinetic energy, $\langle T\rangle$. Use this to find approximate minimum value of $V_0a^2$ required for a bound state to exist. |
 |
|
|
22-04-06 16:04:21 |
n |
|
|
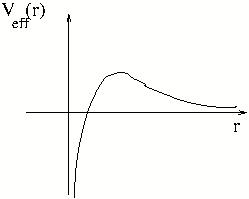
[QUE/CM-05001]Node id: 2876page Read the following discussion of conditions under which a particle can fall to centre in a spherically symmetric potential and answer the question \(\langle \text{\TheFile}\rangle\) at the end.
| Fall to Center |
|
Let V(r) be finite as r $\longrightarrow$ 0. Then $V_\text{eff}(r)
\longrightarrow
\infty$ as $r\longrightarrow 0$ and a particle cannot reach
r=0 for any value of \(E\). However, for certain singular potentials the
particle can reach center. Consider, for example, the case of a potential $V =
\frac{-g}{r^{4}}, \quad g > 0$. Then the effective potential is
\begin{equation}
V_\text{eff} = \frac{-g}{r^{4}} + \frac{L^{2}}{2mr^{2}}
\end{equation}
A sketch of the effective potential is shown in \Figref{cm-drw-0502}.
If $ E > \text{ maximum of }\ V_\text{eff}$, then a particle coming from large distance can fall to center.
|
 |
Question
A criticism of Rutherford model of atom is that an electron will keep loosing energy due to radiation. The radius of its orbit will become shorter and shorter and eventually it will fall to the nucleus.
How do we understand this statement in light of above discussion of fall to centre?
Remember that for Coulomb potential the effective potential is infinite at \(r=0\), if angular momentum is nonzero. |
|
22-04-06 16:04:32 |
n |
|
|
[QUE/CM-04001]Node id: 2554page
- Obtain the Lagrangian for a system with Hamiltonian given by \[ H= \frac{p^2}{2\alpha} - b pq e^{-\alpha t} + \frac{ba}{2}q^2 e^{-\alpha t}(\alpha + be^{-\alpha t} ) + \frac{1}{2} k q^2\]
- Find condition(s) relating parameters \(a\) and \(\alpha\) such that the Lagrangian \(L\) of the system can be written as another Lagrangian \(L_1\) up to a total time derivative of some function \(\Omega\), {\it i.e.}, \[ L-L_1= \frac{d\Omega}{dt}.\] and where \(\Omega\ne0\).
Using the new Lagrangian \(L_1\) find a constant of motion for the system.
|
|
22-04-06 15:04:28 |
n |
|
|
[QUE/QFT-15001] Pair creation probability per unit volumeNode id: 2208pageProve that the probability per unit volume per unit time that the external
potential
\[ \vec{A}= (0,0,a\cos\omega t), A_0=0\]
creates an electron-positron pair in the vacuum is given by
\[ R = \frac{2}{3} \frac{e^2}{4\pi} \Big(\frac{|a|^2}{2} \Big) \omega^2 \Big(
1+ \frac{2m^2}{\omega^2}\Big) \sqrt{1- \frac{4m^2}{\omega^2}} \]
Source :Sakurai
|
|
22-04-06 15:04:31 |
n |
|
|
[QUE/CM-10002]Node id: 2887page
- Show that \begin{equation} Q=-p ,\qquad P=q + Ap^2 \end{equation} (where A is any constant) is a canonical transformation,
- (i) by evaluating \([Q,P]_{q,p}\)
- (ii) by expressing \(pdq-PdQ\) as an exact differential \(dF(q,Q)\). Hence find the type one generating function of the transformation. To do this, you must first use the transformation to express \(p,P\) in terms of \(q,Q\).
- Use the relation \(F_2=F_1+PQ\) to find the type 2 generating function \(F_2(q,P)\),and check your result by showing that \(F_2\) indeed generates the transformation.
Source : Calkin
|
|
22-04-06 15:04:53 |
n |
|
|
[QUE/CM-10003]Node id: 2889pageThe Hamiltonian for a particle moving vertically in a uniform gravitational field \(g\) is \[H=\frac{p^2}{2m} + mgq\]
- Find the new Hamiltonian for new canonical variables \(Q,P\) given by \[ Q=-p, P=q+Ap^2\] Show that we can eliminate \(Q\) from the Hamiltonian (make \(Q\) cyclic) by choosing a constant \(A\) appropriately.
- With this choice of \(A\) write down and solve Hamilton's equations for the new canonical variables, and then use the transformation equations to find the original variables \(q,p\) as functions of time.
Source:Calkin |
|
22-04-06 15:04:29 |
n |
|
|
[QUE/CM-10004]Node id: 2890page
- Show that \begin{equation} Q= q\cos\theta - \frac{p}{m\omega} \sin\theta,\qquad P=m\omega q \sin\theta + p \cos\theta \end{equation} is a canonical transformation
- (i) by evaluating \([Q,P]_{q,p}\)
- (ii) by expressing \(pdq-PdQ\) as an exact differential \(dF_1(q,Q,t)\).Hence find the type 1 generating function of the transformation. To do this you must first express \(p,P\) in terms of \(q,Q\).
- Use the relation \(F_2=F_1+PQ\) to find the type 2 generating function \(F_2(q,P)\), and check your result by showing that \(F_2\) indeed generates the transformation.
Source:Calkin
|
|
22-04-06 15:04:06 |
n |
|
|
[QUE/CM-10005]Node id: 2891pageSuppose that \(q,p\) defined by
\begin{equation}
Q= q\cos\theta - \frac{p}{m\omega} \sin\theta,\qquad P=m\omega q
\sin\theta + p \cos\theta
\end{equation}
are the canonical variables for a simple harmonic oscillator with Hamiltonian
\[ H=\frac{p^2}{2m} +\frac{1}{2}m \omega^2 q^2\]
- Find the Hamiltonian \(K(Q,P,t)\) for the new canonical variables \(Q,P\), assuming that \(\theta\) is some function of time \(\theta(t)\). Show that we can choose \(\theta(t)\) so that \(K=0\).
- With this choice of \(\theta(t)\) solve the new canonical equations to find \(Q,P\) as functions of time, and then use the transformation equations to find the original variables \(q,p\) as functions of time.
Source: Calkin
|
|
22-04-06 15:04:03 |
n |
|
|
[QUE/CM-10006]Node id: 2892page
- Show that the Hamiltonian for a simple harmonic oscillator is invariant under the canonical transformation \begin{equation} Q= q\cos\theta - \frac{p}{m\omega} \sin\theta,\qquad P=m\omega q \sin\theta + p \cos\theta \end{equation} for constant \(\theta\).
- Find the associated constant of motion.
Source:Calkin
|
|
22-04-06 15:04:12 |
n |
||Message]