|
|
[QUE/TH-08004] TH-PROBLEMNode id: 5184pageConsider a system consisting of $N_1$ atoms of Neon gas, of mass $m_1$ and $N_2$ atoms of Argon gas of mass $m_2$ are in a box a volume $V$. The system is in thermal equilibrium at temperature $T$. Treating them as ideal gas, find the entropy $S$ and the Gibbs free energy $G$ of the system.[ Assume the arbitrary solution of Gibb for the resoultion of the Gibbs paradox]. Answer to be in terms of $N_1\,,\,N_2\,,\,m_1\,,\,m_2\,,\,T$ and the fundamental concepts $h$ and $k$
|

|
22-01-14 13:01:59 |
n |
|
|
[QUE/TH-08003] TH-PROBLEMNode id: 5183page
$$pV\,=\,A(T)\,+\,B(T)p\,+\,C(T)p^2 $$
Find $C_p(T,p)$ in terms of $C_p(T,p_0)$ and $p\,,\,p_0$ ( initial and the final pressures) and $A(T)\,,\,B(T)\,,\,C(T)$ and their derivatives with respect to temperature $T$. [ Write an appropriate expression for
$$\frac{\partial C_p}{\partial p} $$ and use it to obtain $C_p$]
|

|
22-01-14 13:01:49 |
n |
|
|
[QUE/TH-07003] TH-PROBLEMNode id: 5182pageShow that the internal energy of a material whose equation of state is
$$ P\,=\,f(V) T $$
is independent of the volume. ( $P$ and $T$ are the pressure and the temperature of the material)
|

|
22-01-14 13:01:14 |
n |
|
|
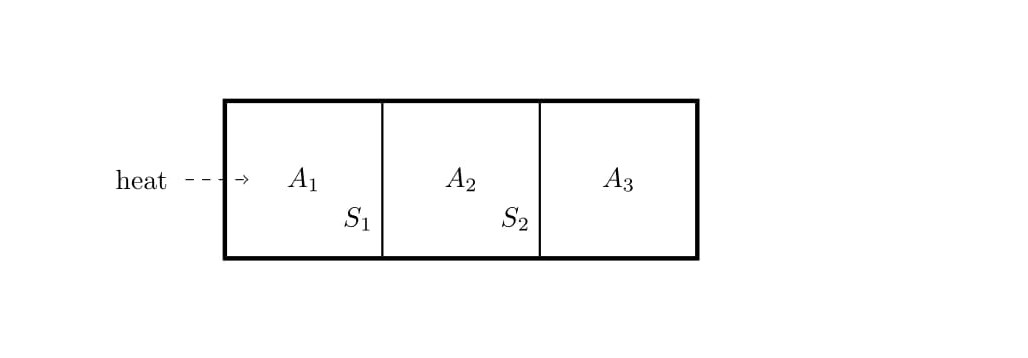
[QUE/TH-02001] TH-PROBLEMNode id: 5040pageConsider a closed cylinder whose walls are adiabatic. The cylinder is divided into three equal parts $A_1$, $A_2$ and $A_3$ by means of partitions $S_1$ and $S_2$, which can move along the length of the cylinder without friction. The partition $S_1$ is adiabatic and $S_2$ is conducting. Initially, each of the three parts contain one mole of Helium gas, which can be treated as an ideal gas, is at pressure $P_0$, temperature $T_0$ and volume $V_0$. Assume the specific heat at constant volume $C_v\,=\,\frac{3R}{2}$ and the specific heat at constant pressure $C_p\,=\,\frac{5R}{2}$. Now, heat is supplied to the to the left most partition $A_1$ till the temperature in part $A_3$ becomes $T_3\,=\,\frac{9T_0}{4}$ Find the final volume, pressure and temperature in terms of $V_0$, $P_0$ and $T_0$. Assume the entire process is quasistatic.
\vskip 3mm
3. ( Continuation of problem 2)
(a) What is work done by the gas in $A_1$ ?
(b) What is the heat supplied to the gas in $A_1$?
|

|
22-01-14 10:01:44 |
n |
|
|
[QUE/TH-05003] TH-PROBLEMNode id: 5158pageConsider $n$ mole of ideal gas whose entropy is given by $$ \frac{n}{2}\left[c_1\,+\,5R{\ln}\frac{U}{n}\,+\,2R{\ln}\frac{V}{n} \right]$$ where $R$ is the univeral gas constant, $U$ the internal energy, $V$ the volume and $c_1$ a constant.
- Calculate the specific heats $c_V$ and $c_p$
- A room is at a temperature $273^o$ K which is in equilbrium with the surroundings. One hour after turning on a heater, the room is at $300^o$ K. Assuming the air is described by the equation given above, find the energy density for the two different temperatures. Answer should be in terms of the atmospheric pressure $P_0$, assume it is constant and the room is always at $P_0$.
|

|
22-01-14 10:01:59 |
n |
|
|
[QUE/SM-06001] SM-PROBLEMNode id: 3217page{Consider an open system of non-interacting particles obeying Maxwell-Boltzmann statistics. The system is at temperature $T$ and chemical potential $\mu$. Let $\sigma^2_N$ denote the variance of the number of particles in the system. Show that \begin{eqnarray*} \sigma^2_N &=& k_BT\left( \frac{\partial\langle N\rangle}{\partial\mu}\right)_{T,V}, \end{eqnarray*} where $\langle N\rangle$ is the mean number of particles. The angular brackets denote averaging is carried out over a grand canonical ensemble
KPN
|

|
22-01-14 10:01:50 |
n |
|
|
[QUE/SM-06004] SM-PROBLEM Node id: 3219pageConsider a cylindrical system of ideal gas with a movable piston as shown . All the wall.\, including the piston are thermally insulating. A weight W is placed on the piston. Treating this system as a closed one, Show that $$ \frac{W}{A}\,=\,\frac{2E}{3V}$$ where A is the area of cross section of the cylinder, E the energy and V the volume of gas.
|

|
22-01-14 10:01:41 |
n |
|
|
[QUE/SM-06003] SM-PROBLEM Node id: 3218pageCalculate $Z_V$ for a classical ideal gas and use it to calculate $(\Delta V)^2 \,=\,\overline{V^2}\,-\,\overline{V}^2 $.
|

|
22-01-14 10:01:18 |
n |
|
|
[QUE/SM-02006] SM-PROBLEMNode id: 5148pageConsider a 2 dimensional phase space ( $q,p$) with a rectangular region defined by four corners as shown.
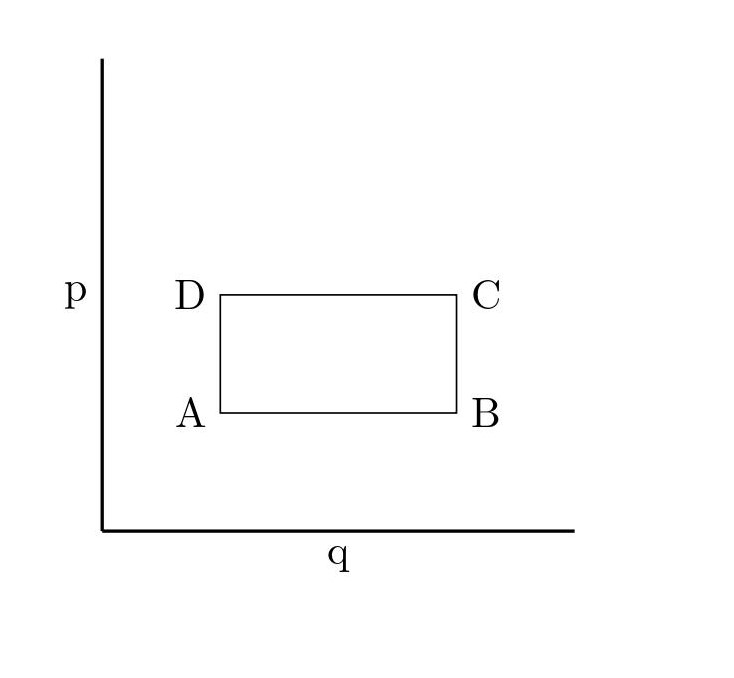
If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is
$$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$
and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively
|

|
22-01-14 10:01:19 |
n |
|
|
[QUE/SM-02001] SM-PROBLEMNode id: 5054pageConsider a 2 dimensional phase space ( $q,p$) with a rectangular region defined by four corners as shown.
If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is
$$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$
and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively
|

|
22-01-14 10:01:53 |
n |
|
|
[QUE/TH-06008] TH-PROBLEMNode id: 5181pageA Carnot engine is made to operate as a refrigerator, operating at $0^o$ C and discharging heat at $20^o$C. Find the minimum amount of work done by the refrigerator in converting one kilogram of water at $0^o$ into ice. ( Assume latent heat to be $L\,=\, 3.35\times 10^5J/Kg.$)
|

|
22-01-14 10:01:51 |
n |
|
|
[QUE/TH-06006] TH-PROBLEMNode id: 5179pageConsider a paramagnetic system, with variables magnetization $M$, the magnetic field $B$ and absolute temperature $T$. ( We assume it's dependence on pressure as negligible). The equation of state is ( which will be obtained from statistical mechanics later in the course) is
$$ M\,=\,C\frac{B}{T}, $$
where $C$ is a constant ( referred to as the Curie constant, who had experimentally obtained this relation.
The system's internal energy is ( for a one-dimensional system)
$$ U\,=\,-MB.$$
The work done on the system by external surrounding is $-MdB$
(a) Write the expression for $DQ$ in terms of $dM$ and $dB$
(b) Write the equation for entropy change $dS$ in terms of $dM$ and $dB$
(c) Obtain the entropy $S$
|

|
22-01-14 09:01:31 |
n |
|
|
[QUE/TH-03003] TH-PROBLEMNode id: 5177pageCalculate the work done when a van der Waals gas of volume $V_1$ expands to a volume $2V_1$ under (a) Constant temperature (b) Under constant pressure. The equation of the gas is
$$ \left(p\,+\,\frac{an^2}{V^2}\right)\left(V\,-\,nb\right)\,=\,nRT $$
where the symbols have the usual meanings. $a$ and $b$ are constants/
|

|
22-01-14 09:01:06 |
n |
|
|
[QUE/SM-01005] SM-PROBLEMNode id: 5149pageUsing the identity $\Gamma(N\,+\,1)\,=\,N!=\,\int_0^\infty x^Ne^{-x} dx $
and write the integral in the form
$$ \int_0^\infty e^{Ng(x)}dx $$
Find the maximum of $g(x)$ ( which occurs say at $x_0$ ). Assume the integral
is dominated by the contribution from the neighbourhood of $x_0$ for large N. Expanding $g(x)$ up to second order in $(x-x_0)$ derive the Stirling's approximation ( for $n\rightarrow\,\infty$)
$$ \rm{ln}N!\,=\,N\rm{ln}N\,-\,N\,+\,\frac{1}{2}\rm{ln}(2\pi N)$$
( More exact formula , just for information, is
$$ N!\,=\,\left(\sqrt{2\pi}\right)e^{-N}N^{N+1/2}\left[1\,+\,\frac{1}{12N}\,+\,\frac{1}{288N^2}\,+\,\ldots\right]$$
|

|
22-01-13 23:01:49 |
n |
|
|
[QUE/TH-06004] TH-PROBLEMNode id: 5163pageCD consists of two adiabatic processes and an isobaric process and an isochoric process of a box of volume V containing perfect gas as shown below
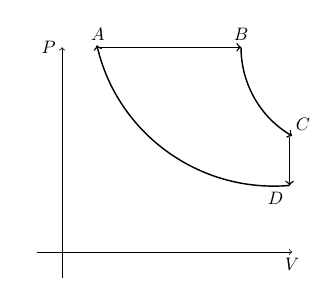
AB is constant volume BC and DA and adiabatic and CD is at constant volume.
Calculate the efficiency of the engine in terms of $V_A$, $V_B$, $V_C$ and the ratio of specific heats $\gamma$.
Remark : The efficency depends upon the equation of state of the system. had we used some other system ( like a gas of photons, whose equation of state, we will discuss soon) the answer is different). Only for carnot's cycle, the efficency is independent of the system.)
|

|
22-01-13 18:01:39 |
n |
|
|
[QUE/TH-01001] TH-PROBLEMNode id: 5151pageShow that constant volume thermometers using an ideal gas as well as a van der Waals gas both yield the same
temperature scale when uniform scales are adopted. Equation of state for ideal gas is \(P V = nRT\) and for van der
Wall gas is
\begin{equation*}
\Big(p + \frac{an^2}{V^2}\Big )(V − nb) = nRT
\end{equation*}
|

|
22-01-13 18:01:52 |
n |
|
|
[QUE/TH-01002] TH-PROBLEMNode id: 5152pageA bimetallic strip of total thickness $x$ is straight at temperature $T$. What is the radius of curvature of the strip,
$R$, when it is heated to temperature $T + ∆T$ ? The coefficients of linear expansion of the two metals are $α_1$ and $α_2$ ,
respectively, with \(α_1 > α_2 \). Assume each metal has thickness \(x/2\), and that \(x << R.\)
|

|
22-01-13 18:01:05 |
n |
|
|
[QUE/TH-03001] TH-PROBLEMNode id: 5154pageConsider \(N\) molecules of a gas obeying van der Waals
equation of state given by
\[\left(P+ \frac{a N^2}{V^2}\right)\big(V-Nb\big)
= Nk_B T\]
where \(a\) is a measure of the attractive forces between
the molecules and \(b\) is another constant proportional to
the size of a molecule. The other symbols have their
usual meanings. Show that during an isothermal expansion (Temperature is kept
constant) from volume \(V_1\) to
volume \(V_2\) quasi-statically and reversibly, the work done is
\[ W =-Nk_B T \log\left(\frac{V_2-Nb}{V_1-Nb}\right) + a^2
\Big(\frac{1}{V_1}-\frac{1}{V_2}\Big)\]
|

|
22-01-13 18:01:03 |
n |
|
|
[QUE/TH-03002] TH-PROBLEMNode id: 5155pageAn ideal gas is enclosed in a cylindrical volume with a movable piston. It can be taken from a state 1 to state 2 by several processes as shown in \(P-V \) diagram below. It is given that if the walls are adiabatic the system obeys the equation \(P^3 V^5=\text{const}\) The energy of the state in state 1 is given to be 100J. The pressures and volume at for the two states are given as follows. \[P_1=10^5 \,\text{Pa}, V_1=10^{-3}\, \text{m}^3; P_2 =\Big(\frac{10^5}{32}\Big) \,\text{Pa}, V_2= b\times 10^{-3}\, \text{m}^3.\] {\textwidth}{ Several paths taking the system from state 1 to state 2 are shown in figure below.
- AB followed by BC
- AD followed by DC
- Linear path connecting A and C
- Some other path AQC
Your are required to compute the internal energy of the system in state 2 by computing work done by selecting a path from one of the above options. If you choose option (d), some other path, specify the path. Compute the work done along the path chosen and find the internal energy of system in state 2.
|

|
22-01-13 18:01:59 |
n |
|
|
[QUE/TH-06006] TH-PROBLEMNode id: 5062page Consider a photon gas in two dimensions at temperature T in area A. Find the energy density $u(\omega)$ as a function of temperature and various physical constants. Show that the total energy is proportional to $T^3$. ( you can assume that the internal degree of freedom is 1. )
|

|
22-01-13 18:01:29 |
n |