|
|
[ QUE/SM-03003] SM-PROBLEM Node id: 2217page
Consider tossing of N independent coins.
- What is the micro state space associated with this experiment ?
- Write down explicitly the elements of the micro state space for experiments with \(N = 2\) and \(N = 3\).
- Let \(\hat{\Omega(N)}\) denote the micro state space and \{\Omega(N)\} the number of elements of \(\hat{\Omega}(N)\), calculate \(\Omega(N)\).
KPN
|

|
22-01-07 11:01:13 |
n |
|
|
[QUE/SM-03007] SM-Problem Node id: 2215page
Consider a system of $N$ atoms. Assuming that they can exist in two states only.
The ground state having energy zero and an excited state having energy \(\epsilon\).
- Find the number of micro states with total energy \(U\).
- Write an expression for entropy and using Stirling approximation for the factorial \[ \ln (N!) \approx N \ln N - N\] find the temperature of the system and hence show that \[U = \frac{N\epsilon}{1+ e^{\epsilon/kT}}\] What is fraction of atoms are in the excited state at very large temperature \((T >> kT)\)?
|

|
22-01-07 11:01:37 |
n |
|
|
[QUE/SM-03008] SM-PROBLEM Node id: 2216page In a monoatomic crystalline solid each atom can occupy either a regular lattice site or an interstitial site. The energy of an atom at an interstitial site exceeds the energy of a atom at a lattice site by an amount \(\epsilon\). Assume that the number interstitial sites equals the number of lattice sites, and also equals the number of atoms \(N\).
Calculate the entropy of the crystal in the state where exactly \(n\) of the atoms are at the interstitial sites. What is the temperature of the crystal in this state, if the crystal is in thermal equilibrium?
If \(\epsilon=1 \text{ ev}\) and the temperature of the crystal is 300K, what is the fraction of the atoms at the interstitial sites?
MANDL
|

|
22-01-07 11:01:18 |
n |
|
|
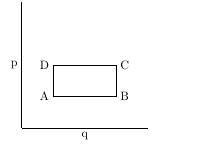
[QUE/SM-03013] SM-Problem Node id: 3252page
| If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is $$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$ and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively. |
 |
|

|
22-01-07 11:01:13 |
n |
|
|
[QUE/SM-02007] SM-PROBLEM Node id: 3258pageShow that the expression below could not have come from an equation of state. \[ dP= C_1 \Big\{\frac{2(v-b)}{RT}dv + \frac{(v-b)^2}{RT^2} dT\Big\}\]
( \(P\) is pressure, \(v\) is specific volume, \(T\) the temperature, \(R\) the gas constant , $C_1$ , \(a, b\) are dimensioned constants )
HSMani
|

|
22-01-07 10:01:23 |
n |
|
|
[QUE/SM-02002] SM-PROBLEM Node id: 3226pageA thermally insulated chamber contains $1000$ moles of mono-atomic ideal gas\footnote{$PV=nRT$} at $10$ atm. pressure. Its temperature is $300$ K. The gas leaks out slowly through a valve into the atmosphere. The leaking process is quasi static, reversible and adiabatic \(^\)1
- How many moles of gas shall be left in the chamber eventually?
- What shall be the temperature of the gas left in the chamber ?
$1$ atm $=0.981\times 10^6$ Pa ; $\gamma={\displaystyle \frac{C_P}{C_V}=\frac{5}{3}}$ .
Footnote 1 :: $PV^\gamma=\Theta$ where $\Theta$ is a constant.}. KPN
|

|
22-01-07 10:01:02 |
n |
|
|
[QUE/SM-02008] SM-PROBLEM Node id: 3259pageThe following equations are purported to be fundamental equations of various thermodynamic systems Find the one's which are not physically permissible and which postulate is violated. $$ S\,=\,\left(\frac{R^2}{v_0\theta}\right)^{1/3}\left[NUV\right]^{1/3} $$ $$ S\,=\,\left(\frac{R}{\theta^2}\right)^{1/3}\left[\frac{NU}{V}\right]^{2/3} $$ $$ S\,=\,\left(\frac{R}{\theta}\right)^{1/2}\left[NU\,+\,\frac{R\theta\,V^2}{v_0^2} \right]^{1/2}$$ S,U,V and N have the usual meanings $v_0$, $\theta$ and R are constants.
HSMani
|

|
22-01-07 10:01:34 |
n |
|
|
[QUE/SM-02003] SM-PROBLEM Node id: 3227pageA particular system obeys the fundamental equation, $$U=A\ \frac{N^3}{V^2}\exp\left( \frac{S}{Nk_B}\right), $$ where $A$ (joule metre$^2$) is a constant. Initially the system is at $T=317.48$ kelvin, and $P=2\times 10^5$ pascals. The system expands reversibly until the pressure drops to $10^5$ pascals, by a process in which the entropy does not change. What is the final temperature ?
KPN
|

|
22-01-07 10:01:07 |
n |
|
|
[QUE/SM-02005] SM-Problem Node id: 3229page
Consider a gas contained in a cylindrical enclosure with a piston attached to a spring ( spring constant K )
Initially the gas is at 200 kilo Pascal ( kPa) and occupies a volume of $0.1 m^3$. The atmospheric pressure is 100 kPa . The gas is heated until the volume is doubled and the final pressure is 500 kPa. The spring exerts a force proportional to the displacement from its equilibrium position. Calculate the work done by the gas |
 |
|

|
22-01-07 10:01:45 |
n |
|
|
[QUE/SM-02010] SM-PROBLEM Node id: 3225pageConsider one mole of an ideal gas. A molecule of the gas is mono atomic and is spherically symmetric. The system of ideal gas is in equilibrium. Its temperature $T_1=300$ k and its volume $V_1=1$ litre. Since the system is in equilibrium, it can be represented by a point $A=( V_1,T_1)$, in the temperature-volume thermodynamic phase plane. We are taking Volume along the $X$ axis and Temperature along the $Y$ axis.
Now consider a process by which the system expands to a volume $V_2=2$ litres. The process is adiabatic.
- {\bf Case-1 :} The process is quasi static and reversible. Let $T_2$ be the temperature of the system at the end of the process. Let $B=(V_2,T_2)$ denote the system at the end of the process. {\bf Find} $T_2$. The process $A\to B$ can be represented by a curve joining $A$ to $B$. The curve is called an adiabat.
- {\bf Case-2 :} The process is not reversible. Hence the process can not be represented by a curve in the thermodynamic phase diagram. The system disappears from $A$ at the start of the process. At the completion of the process, if we wait long enough, the system would equilibrate and appear at a point $B^\prime=(T_2^\prime,V_2)$ in the phase diagram. There is no ready-made formula for calculating $T_2^\prime$. Nor is there a formula for calculating the increase in entropy of the system in the irreversible process. Also these quantities depend on how far away the irreversible process is from its reversible companion. However $B^\prime$ is on a line parallel to $Y$ axis and passing through $B$. Employing the Second law of thermodynamics
Answer the following questions.
- Find if the point $B^\prime$ is vertically above or below the point $B$.
- Calculate the increase in entropy in terms of $T_2^\prime$.
|

|
22-01-07 10:01:16 |
n |
|
|
[QUE/SM-04002] SM-PROBLEM Node id: 3235pageThere are three single particle quantum levels : a {\bf non} degenerate ground state of energy zero and a doubly degenerate excited state of energy $\epsilon=10k_B\ln 18$ joules. Non-interacting particles obeying Maxwell-Boltzmann statistics occupy these three quantum levels. The closed system is described by a canonical ensemble at temperature $T$. Find the temperature below which more than $90$ percent of the particles would be found in the ground state.
KPN
|

|
22-01-07 10:01:49 |
n |
|
|
[QUE/SM-02009] SM-PROBLEM Node id: 3260pageThe article ( Physics Today 32,(2000) by Elliot Lieb and Jacob Yngvason titled " A Fresh Look at Entropy and the Second Law of Thermodynamics") write "... We use it to calculate entropy, specific and latent heat, phase transition properties, transport coefficients , and so on,with great accuracy.
Important examples abound, such as Max Planck's realization that by staring into the furnace he could find Avogadro's number and Linus Pauling's highly accurate back of the envelope calculation of the residual entropy of Ice.
" What method could Max Planck used to get the Avogadro number?
( Linus Pauling's calculation will be discussed later.)
Please read the article by Lieb and Yngvason, it only 6 page long.
HSMani
|

|
22-01-07 10:01:29 |
n |
|
|
[QUE/SM-02004] SM-PROBLEM Node id: 3228pageThere are $N$ ideal gas molecules in a room of volume $V=10\ {\rm M}^3$ and at room temperature. The molecules are in equilibrium. There is an imaginary box of volume $v\ {\rm M}^3$ completely contained within the room. The walls of the box are permeable and conducting. In other words, the box exchanges energy and matter with its surroundings. Let $\nu$ denote a random variable defined as the number of molecules in the box. Let $P(n)$ be the probability that $\nu=n$. Let $\mu=Nv/V$. Derive appropriate expressions for $P(n)$ to describe the statistics of $n$ for the following cases :
| (i) $v=6\ {\rm M}^3$ and $N=10$ |
(ii) $v=10\ {\rm cm}^3$ and $N=10^5$ |
Calculate the mean and variance of the random variable $\nu $ for both cases.
|

|
22-01-07 10:01:07 |
n |
|
|
[QUE/SM-05001] SM-PROBLEM Fermi Dirac DistributionNode id: 5146pageShow from calculating
$$ \frac{\Delta S}{\Delta E}\,=\,\frac{1}{T}\,=\,k\beta$$
for the case of Fermi-Dirac distribution,
$$ \Omega_{FD}\,=\,\Pi_{i=1}^\infty\left({}^{g_i}C_{N_i}\right) $$
[ notation as used in the class ]. Also for the case of equilibrium we have
$$ N_i\,=\,\frac{g_i}{e^{\alpha+\beta\epsilon_i}\,+\,1} $$
Hint: Consider changes only in two levels say with energies $\epsilon _1$ and $\epsilon_2$. Then argue that the result so obtained is independent of the choice of levels]
|

|
22-01-07 09:01:25 |
n |
|
|
Statistical Mechanics --- Notes for Lectures and Problems [SM-MIXED-LOT]Node id: 4690collectionStatistical Mechanics
Mixed Lot of Problems in Statistical Mechanics
- SM-Mod01 Probability and Statistics
- SM-Mod02 Thermodynamics -- Review Problems
- SM-Mod03 Microcanonical Ensemble
- SM-Mod04 Canonical Partition Function
- SM-Mod05 Application to Nondegenerate Perfect Gases
- SM-Mod06 Grand Canonical Partition Function
- SM-Mod-08 Statistical Mechanics of Photons
- SM-Mod09 Statistical Mechanocs of Fermions
- SM-Mod10 Perfect Boson Gas; Bose Einstein Condensation
|

|
22-01-06 21:01:50 |
n |
|
|
Classical Mechanics --- Notes for Lectures and Problems [CM-MIXED-LOT] Node id: 4687collectionNOTES FOR LECTURES ON CLASSICAL MECHANICS
- NOTES/CM-01 Topics in Newtonian Mechanics
- NOTES/CM-02 Analytical Mechanics
- NOTES/CM-03 Action Principle
- NOTES/CM-04 Hamiltonian Form of Dynamics
- NOTES/CM-05 Spherically Symmetric Potentials
- NOTES/CM-06 Scattering
- NOTES/CM-07 Small Oscillations
- 7.1 Small Oscillations in One Dimension
- 7.2 Small Oscillations
- 7.3 Some Experiments on Small Oscillations
- 7.4 Lagrangian Formualtion of Small Oscillations
- 7.5 A Model of Vibrating Crystals
- NOTES/CM-08 Galilean Transformations, Non Inertial Frames
- 8.1 Rotations about Coordinate Axes
- NOTES/CM-09 Rigid Body Dynamics
- NOTES/CM-10 Canonical Transformations
- LEC/CM08-001 Canonical Transformations
- LEC/CM-08-002
- LEC/CM-08-003
- NOTES/CM-11 Hamilton Jacobi Theory
|

|
21-12-30 22:12:02 |
n |
|
|
Group Theory --- Notes for Lectures and of Problems [GT-MIXED-LOT]Node id: 4705collection |

|
21-12-30 22:12:50 |
n |
|
|
Quantum Information and Quantum Computing --- Notes for Lectures and Problems [QIQC-MIXED-LOT]Node id: 5064collection |

|
21-12-30 22:12:13 |
n |
|
|
Elementary Particle Physics --- Notes for Lectures and Problems [EPP-MIXED-LOT]Node id: 4703collectionElementary Particle Physics
|

|
21-12-30 22:12:34 |
n |
|
|
EPP-Problem --- Id:: QUE/EPP-01006Node id: 2631pageThe mass of pion can be determined from measurements of kinetic energy of neutron in the reaction \[ \pi^- + p \longrightarrow n + \pi^0.\] The \(\pi^-\) meson falls in Bohr orbit, (S state), before being captured by the proton. Neglecting the kinetic energy of the pion show that \begin{eqnarray} T_n &=& \sqrt{\omega^2 + M_n^2} - M_n\\ \omega &=& \frac{1}{2}\Big[ M_p + m_{\pi^-} - \frac{M_n^2}{M_p+ M_{\pi^-}} \Big]. \end{eqnarray}
The kinetic energy of the neutron is found to be \(T_n=8.872 \)MeV. Use this data to determine the mass difference \(m_{\pi^-}-m_{\pi^0}\)
|

|
21-12-23 19:12:39 |
n |