Notices
 

QUE/SM

For page specific messages
For page author info
Title Name Datesort ascending

[QUE/SM-06001] SM-PROBLEM

{Consider an open system of non-interacting particles obeying Maxwell-Boltzmann statistics. The system is at temperature $T$ and chemical potential $\mu$. Let $\sigma^2_N$ denote the variance of the number of particles in the system. Show that \begin{eqnarray*} \sigma^2_N &=& k_BT\left( \frac{\partial\langle N\rangle}{\partial\mu}\right)_{T,V}, \end{eqnarray*} where $\langle N\rangle$ is the mean number of particles. The angular brackets denote averaging is carried out over a grand canonical ensemble

KPN

 kapoor's picture 22-01-14 10:01:50

[QUE/SM-06004] SM-PROBLEM

Consider a cylindrical system of ideal gas with a movable piston as shown . All the wall.\, including the piston are thermally insulating. A weight W is placed on the piston. Treating this system as a closed one, Show that $$ \frac{W}{A}\,=\,\frac{2E}{3V}$$ where A is the area of cross section of the cylinder, E the energy and V the volume of gas.

 kapoor's picture 22-01-14 10:01:41

[QUE/SM-06003] SM-PROBLEM

Calculate $Z_V$ for a classical ideal gas and use it to calculate $(\Delta V)^2 \,=\,\overline{V^2}\,-\,\overline{V}^2 $.

 kapoor's picture 22-01-14 10:01:18

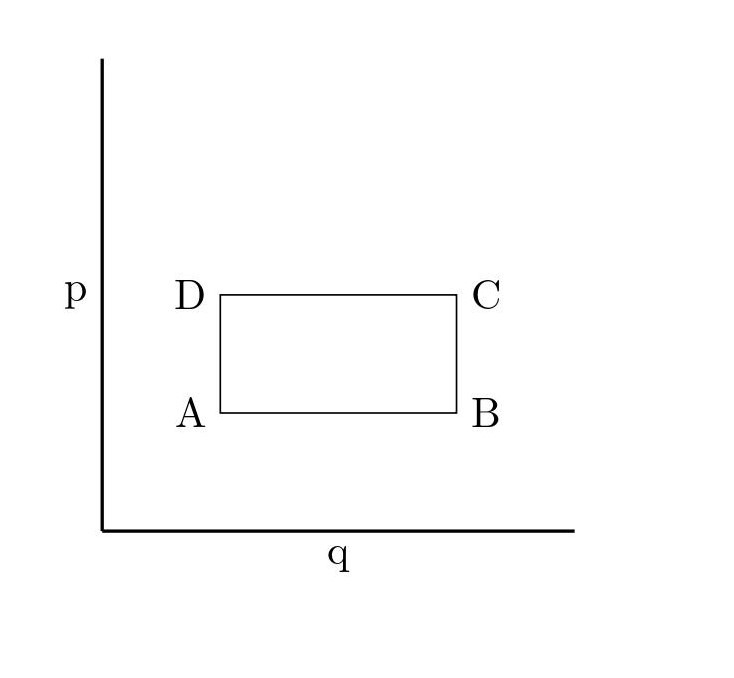
[QUE/SM-02006] SM-PROBLEM

Consider a 2 dimensional phase space ( $q,p$) with a rectangular region defined by four corners as shown.

If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is
$$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$
and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively

 AK-47's picture 22-01-14 10:01:19

[QUE/SM-02001] SM-PROBLEM

Consider a 2 dimensional phase space ( $q,p$) with a rectangular region defined by four corners as shown.
If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is
$$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$
and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively

 AK-47's picture 22-01-14 10:01:53
 
X