[QUE/SM-02006] SM-PROBLEM

Consider a 2 dimensional phase space ( $q,p$) with a rectangular region defined by four corners as shown.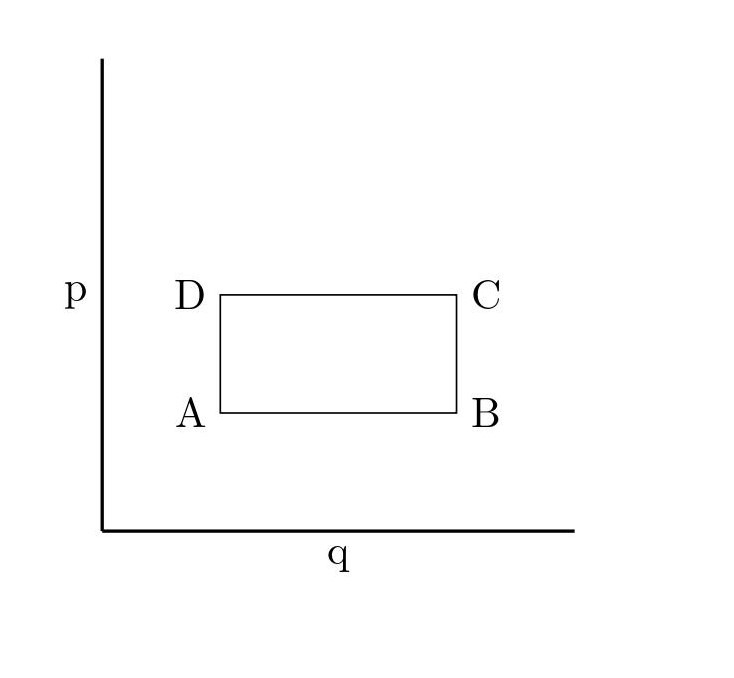

If the region ABCD is the phase space region at time time t = 0 , find the region $A'B'C'D'$ at time t given the Hamiltonian is
$$ H\,=\,\frac{p^2}{2m}\,-\, m a q $$
and explicitly verify that the area is constant. Take the coordinates of A,B,C and D as $(q_A,p_A)\,,\,(q_B,p_A)\,,\,(q_B,p_C)$ and $(q_A,p_C)$ respectively