[NOTES/QM-13002] The S -matrix in One Dimensional Potential Problems

Definition

Consider motion in one dimensional potential \(V(x)\) which tends to zero for large \(x\), {\it i.e.} as \(x\to \pm \infty\). Assume that the energy \(E\) of the particle is positive, so that for large distances the solution of the Schr\"{o}dinger equation is oscillatory and is linear combination of plane waves \(exp(\pm ikx)\). Thus we can write
\begin{eqnarray} \psi(x) =\begin{cases} A \exp(ikx) + B \exp(-ikx) & \text{ as } x \to -\infty\\ C \exp(ikx) + D \exp(-ikx) & \text{ as } x \to \infty \end{cases}\Label{EQ01} \end{eqnarray}
The equation of continuity, {\it i.e.} probability conservation implies that the probability current is constant. Computing \begin{equation}\Label{EQ02} j(x) = \frac{i\hbar}{2m}\Big[\psi^*(x)\dd[\psi]{x}-\psi(x)\dd[\psi^*]{x} \Big] \end{equation} for \(x\to +\infty\) and for \(x\to -\infty\) and equating the answers we get \begin{equation}\Label{EQ03} |A|^2 -|B|^2 = |C|^2 - |D|^2. \end{equation}
We rearrange this equation to write it as \begin{equation}\Label{EQ04} |A|^2 + |D|^2 = |B|^2 + |C|^2. \end{equation} In matrix notation we get \(u^\dagger u= v^\dagger v\), where \(u,v\) are two component column vectors
\begin{equation}\Label{EQ05} u= \mbox{$\begin{pmatrix} A \\ D\end{pmatrix}$}, \qquad v=\mbox{$\begin{pmatrix} C \\ B \end{pmatrix}$}. \end{equation}
Thus the norms of vectors \(u,v\) are equal for all \(A,B,C,D\) and the two vectors will be related by a unitary matrix, called the \(S\) matrix, and denoted by \(S\). \begin{equation}\Label{EQ06} v = S u. \end{equation} Writing it in full matrix form we have \begin{equation} \begin{pmatrix}C\\ B\end{pmatrix} = \begin{pmatrix}S_{11} & S_{12}\\ S_{21} & S_{22}\end{pmatrix}\begin{pmatrix}A\\ D\end{pmatrix} \end{equation}

Incoming and outgoing waves

The case \(B=C=0\) in \eqref{EQ01} corresponds to incoming waves. The case
when \(A=D=\) is called outgoing wave. Thus we write

\begin{eqnarray} \psi_\text{in}(x) &=&{\begin{cases} A \exp(ikx) & \text{ as } x \to -\infty\\ D \exp(-ikx) & \text{ as } x \to \infty \end{cases}}\Label{EQ07}\\ \psi_\text{out}(x) &=&{\begin{cases} B \exp(-ikx) & \text{ as } x \to -\infty\\ C \exp(ikx) & \text{ as } x \to \infty \end{cases}}\Label{EQ08} \end{eqnarray}
Then the \(S\) matrix transforms in states into out states: \begin{equation} \ket{\psi_\text{out}} = S \ket{\psi_\text{in}} \end{equation}

Fig 1 In and Out Going Waves

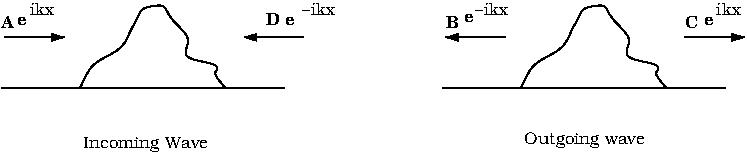Reflection and transmission coefficients

For wave incident from the left \(A=1\) and \(D=0\), then \begin{equation} C=S_{11} \qquad B= S_{21} \end{equation} \(B=S_{12}\) gives the reflection amplitude and \(C=S_{11}\) is the transmission coefficient for the waves incident from the left.

On the other hand, for waves incident from the right, \(D=1, A=0\). In this case \(C=S_{12}\) is the reflection amplitude and \(B=S_{22}\) is the amplitude
for transmission.

Time reversal and $S$ matrix

Using \(\tilde{\psi}\) to denote the time reversed state corresponding to \(\psi\), we have \begin{equation} \psi(x) \xrightarrow{\text{Time Reversal}} \tilde{\psi}(x) = \psi^*(x). \end{equation} Action of time reversal on in and out states, \r{EQ07}-\eqRef{EQ08}, we get

\begin{eqnarray} \tilde{\psi}_\text{in}(x) &=&{\begin{cases} A^* \exp(-ikx) & \text{ as } x \to -\infty\\ D^* \exp(ikx) & \text{ as } x \to \infty \end{cases}}\Label{EQ13}\\ \tilde{\psi}_\text{out}(x) &=&{\begin{cases} B^* \exp(ikx) & \text{ as } x \to -\infty\\ C^* \exp(-ikx) & \text{ as } x \to \infty \end{cases}}\Label{EQ14} \end{eqnarray}

Thus the roles of in and out states get interchanged. Applying the definition of \(S\) matrix to \eqRef{EQ13}-\eqRef{EQ14} we get \begin{equation} \begin{pmatrix}D^*\\ A^*\end{pmatrix} = \begin{pmatrix}S_{11} & S_{12}\\ S_{21} & S_{22}\end{pmatrix}\begin{pmatrix}B^*\\ C^*\end{pmatrix} \end{equation}
Multiplying the matrices on the right we get the following equations
\begin{eqnarray} D^* &=& S_{11} B^* + S_{12} C^*\\ A^* &=& S_{21} B^* + S_{22} C^* \end{eqnarray}
Taking complex conjugate and writing the result in a matrix form again we get
\begin{equation} \begin{pmatrix}C\\B \end{pmatrix} =\begin{pmatrix}S_{22} & S_{12}\\ S_{21} & S_{11}\end{pmatrix} \begin{pmatrix}A\\ D \end{pmatrix} \end{equation}
This gives the \(S\) matrix for time reversed states
\begin{equation} S \xrightarrow{\text{Time Reversal}} \tilde{S} = \begin{pmatrix}S_{22} & S_{12}\\ S_{21} & S_{11}\end{pmatrix}. \end{equation}
Thus we have invariance under time reversal if \(S_{11}=S_{22}\). The form of \(S\) matrix for a model with time reversal symmetry, {\it \i.e.} for real potentials, the \(S\) matrix has the form \begin{equation} S = \begin{pmatrix}S_{11} & S_{12}\\ S_{21} & S_{11}\end{pmatrix}. \end{equation}

Parity and \(S\) matrix

If the potential is an even function of \(x\), the elements of \(S\) matrix
\begin{equation}
S =\begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22}\end{pmatrix}
\end{equation}
obey the conditions \(S_{12}=S_{21}\)
% \MetDat{LUPDate}{Oct 19, 2021}}{qm}{13001}.
For a real potential which is also an even function of \(x\), we have
\(S_{11}=S_{22}, S_{12}=S_{21}\), and we can write the \(S\) matrix in the form \begin{equation} S =\begin{pmatrix} t & r \\ r & t \end{pmatrix} \end{equation} where \(t, r\) are some complex numbers constrained by the unitarity of the \(S\) matrix. The unitarity of the \(S\) matrix requires \begin{equation} |r|^2 +|t|^2=1, \qquad r^*t+t^*r =0 \end{equation}

Question (Try Now)

The \(S\) matrix is unitary, therefore the eigenvalues have the form
\(\exp(i\delta)\). Find the two eigenvalues and relate the two phases,
\(\delta_1,\delta_2\), to the complex numebers \(r, t\).