testing sample

An electron moving with speed of \(5.0\times 10^8\)cm/sec is shot parallel to an electric field strength of \(1.0\times 10^3\)nt/coul arranged so as to retard its motion.

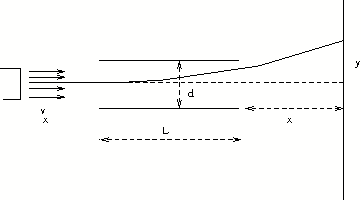
If an ink drop has a mass of \(50\times10^{-9}\) g and is given a charge of \(-200\times 10^{-15}\) C, find vertical displacement in an inkjet printer with 3keV deflection potential, 3mm plate separation and 15 mm deflection plate length. The nozzle ejects the drop with velocity 25 m sec\(^{-1}\) and leaving edge of the deflection plate is at a distance 15 mm from the paper.Source [Kraus p117]

A gold nucleus contains a positive charge equal to that of 79 protons. An \(\alpha\) particle, \(Z=2\), has kinetic energy \(K\) at points far away from the nucleus and is traveling directly towards the  charge, the particle just touches the surface of the charge and is reversed in direction. relate \(K\) to the radius of the gold nucleus. Find the numerical value of kinetic energy in MeV is the radius \(R\) is given to be \(5 \times10^{-15}\) m.

[ 1 MeV = \(10^6\) eV and 1 eV = \(1.6\times10^{-16}\)]

An electron is constrained to move along the axis of a ring of charge \(q\) and radius \(a\). Show that the electron can perform small oscillations along the axis of with time period given by \[T=\frac{1}{2\pi}\frac{4\pi\varepsilon_0 m a^2}{eq}\]

Two pith balls, each of mass 1.8 g, are suspended from the same point
by silk threads each of length 20 cm. When equal charge Q is given to
both the balls, they separate until the two threads become
perpendicular. Find the charge \(Q\) on each pith ball.

An alpha particle travels in a circular path of radius \(0.45\)m in a
magnetic field with \(B=1.2\)w/m\(^2\).
Calculate 
(i) its speed (ii) its period of revolution, and (iii) its kinetic
energy.
Mass of alpha particle = \(6.64424. 10^{-27}\)kg \(\approx 4\times M_p= 4\times938.27\) MeV.

An alpha particle travels in a circular path of radius \(0.45\)m in a magnetic field with \(B=1.2\)w/m\(^2\). Calculate
(i) its speed
(ii) its period of revolution, and
(iii) its kinetic energy.
[Mass of alpha particle =  \(6.64424. 10^{-27}\) kg =3727.4 MeV.]

Anon

An alpha particle travels in a circular path of radius \(0.45\)m in a magnetic field with \(B=1.2\) w/m\(^2\). Calculate (i) its speed (ii) its period of revolution, and (iii) its kinetic energy. Mass of proton particle = \(1.67\times 10^{-27}\)kg \(\approx 4\times M_p= 4\times938.27\) MeV.

Solution :

• [(i)] the magnetic force \(eBv\) must be equal to the mass times acceleration. Therefore \[\begin{equation*} Bev = \frac{Mv^2}{R}, \end{equation*}\] where \(R\) is the radius of the circular orbit. Hence \[\begin{equation*} v= \frac{eBR}{M} = \frac{2\times1.6 \times10^{-19}\times 1.2 \times 0.45}{4\times 1.67\times 10^{-27}}\approx 2.7 \times10^7 \text{m/s}. \end{equation*}\]
• [(ii)] The time period is \[\begin{equation*} T = \frac{2\pi R}{v} = \frac{2\times3.14\times 0.45}{2.7\times10^7} \approx10^{-7} \text{ s}. \end{equation*}\]
• [(iii)] The kinetic energy is given by \[\begin{eqnarray}\nonumber \text{K.E.} &=& \frac{1}{2} M v^2= \frac{1}{2}\times (4\times 1.67 \times 10^{-27}) \times \big(2.7\times10^7\big)^2 \\\nonumber &=& 3.26\times 7.29 \times 10^{-13} \approx 23.7 \times 10^{-13} \text{J}. \end{eqnarray}\]

Find the direction and magnitude of \(\vec{E}\) at the center of a square
with charges at the corners as shown in figure below. Assume that
\(q= 1\times 10^{-8}\)coul, \(a=5\)cm.

A "dipole" is formed from a rod of length \(2a\) and two charges \(+q\)
and \(-q\). Two such dipoles are oriented as shown in figure at the end,
their centers being separated by a distance \(R\). Calculate the force
exerted on the left dipole and show that, for \(R>>a\), the force is
approximately given by
\[F=\frac{3p^2}{2\pi\epsilon_0R^4}\]
where \(p=2qa\) is the dipole moment.

Find the direction and magnitude of \(\vec{E}\) at the center of a square
with charges at the corners as shown in figure below. Assume that
\(q= 1\times 10^{-8}\)coul, \(a=5\)cm.

An electron moving with speed of \(5.0\times 10^8\)cm/sec is shot parallel to an electric field strength of \(1.0\times 10^3\)nt/coul arranged so as to retard its motion.

• How far will the electron travel in the field before coming (momentarily) to rest ?
• how much time will elapse?
• If the electric field ends abruptly after \(0.8\) cm, what fraction of its initial energy will the electron loose in traversing the field?

[1] A thin glass rod is bent into a semicircle of radius \(R\). A charge \(+Q\) is
uniformly distributed along the upper half and a charge \(-Q\) is distributed
uniformly along the lower half as shown in the figure. Find the electric field
at
P, the center of the semicircle.

Three equal charges are placed at the corners of an equilateral triangle.
Show that the electric field at the center is zero.

Sixteen equal charges \(q\) are placed at the corners of a regular polygon of 17 sides. Find the force  exerted by these charges on a  seventeenth charge \(q\) placed at the center of the polygon.

Show that the electric field at the center of a regular \(N\)-sided polygon is <br />zero when equal charges are placed at the corners of the polygon.