1: Repository, 2: PSets, 3:PSN
01 Motion of Point Charges In EM Fields
1
| [QUE/EM-01001] An electron moving with speed of \(5.0\times 10^8\)cm/sec is shot parallel to an electric field strength of \(1.0\times 10^3\)nt/coul arranged so as to retard its motion.
|
||
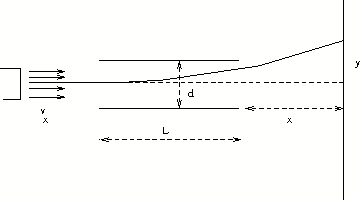
| [QUE/EM-01002] If an ink drop has a mass of \(50\times10^{-9}\) g and is given a charge of \(-200\times 10^{-15}\) C, find vertical displacement in an inkjet printer with 3keV deflection potential, 3mm plate separation and 15 mm deflection plate length. The nozzle ejects the drop with velocity 25 m sec\(^{-1}\) and leaving edge of the deflection plate is at a distance 15 mm from the paper.
[Kraus p117] |
||
| [QUE/EM-01002] --- EM-Solution |
||
| [QUE/EM-01003] --- EM-PROBLEM
|
||
| [QUE/EM-01004] EM-PROBLEM
A gold nucleus contains a positive charge equal to that of 79 protons. An \(\alpha\) particle, \(Z=2\), has kinetic energy \(K\) at points far away from the nucleus and is traveling directly towards the charge, the particle just touches the surface of the charge and is reversed in direction. relate \(K\) to the radius of the gold nucleus. Find the numerical value of kinetic energy in MeV is the radius \(R\) is given to be \(5 \times10^{-15}\) m. [ 1 MeV = \(10^6\) eV and 1 eV = \(1.6\times10^{-16}\)] |
||
| [QUE/EM-01005] Problem-EM --- Small oscillations near a charged ring
An electron is constrained to move along the axis of a ring of charge \(q\) and radius \(a\). Show that the electron can perform small oscillations along the axis of with time period given by \[T=\frac{1}{2\pi}\frac{4\pi\varepsilon_0 m a^2}{eq}\] |
||
| [QUE/EM-01006] --- EM-PROBLEM
|
||
| [QUE/EM-01007] --- EM-PROBLEM |
||
| [QUE/EM-01008] --- EM-PROBLEM
Two pith balls, each of mass 1.8 g, are suspended from the same point by silk threads each of length 20 cm. When equal charge Q is given to |
||
| [QUE/EM-01010] --- EM-PROBLEM
An alpha particle travels in a circular path of radius \(0.45\)m in a magnetic field with \(B=1.2\)w/m\(^2\). |
||
| [QUE/EM-01010] EM-PROBLEM Alpha particle in magnetic field; motion in a circle An alpha particle travels in a circular path of radius \(0.45\)m in a magnetic field with \(B=1.2\)w/m\(^2\). Calculate |
||
| [QUE/EM-01011] --- EM-PROBLEM
An alpha particle travels in a circular path of radius \(0.45\)m in a magnetic field with \(B=1.2\) w/m\(^2\). Calculate (i) its speed (ii) its period of revolution, and (iii) its kinetic energy. Mass of proton particle = \(1.67\times 10^{-27}\)kg \(\approx 4\times M_p= 4\times938.27\) MeV.
|
||
| [QUE/EM-01012] --- EM-PROBLEM
Find the direction and magnitude of \(\vec{E}\) at the center of a square with charges at the corners as shown in figure below. |
||
| [QUE/EM-01013] --- EM-PROBLEM
A "dipole" is formed from a rod of length \(2a\) and two charges \(+q\) and \(-q\). Two such dipoles are oriented as shown in figure at the end, |
||
| [QUE/EM-01014] --- EM-PROBLEM
Find the direction and magnitude of \(\vec{E}\) at the center of a square with charges at the corners as shown in figure below. Assume that |
||
| QUE/EM-01016] --- EM-PROBLEM An electron moving with speed of \(5.0\times 10^8\)cm/sec is shot parallel to an electric field strength of \(1.0\times 10^3\)nt/coul arranged so as to retard its motion.
|
2
3
02 Continuous Charge Distribution
1
2
3
03 Electric Potential and Electrostatic Energy
1
2
05 Maxwell's Equations in Dielectric Medium
1
- LEC/EM-05:: Electrostatics of Dielectric Media






 ||Message]
||Message]