CMI CM-I Problem Sheet 10 (2012)

Barn and Pole paradox: There is barn (BAEFD) of length L (AB = L) in it's rest frame. D is a door which is open initially and can be closed. A person P carrying a pole of rest length L is coming with a velocity V with respect to the barn. Consider the set of events from the barn's frame . The length of the pole would be $\rm{L}/\gamma$ where $\gamma\,=\,(1-\rm{V}^2/c^2)^{-1/2}$ and so concludes that the moment the front end of the pole Y, touches the back of the wall AE he can close the door D as the length of the pole is less than L. (The door D is initially kept open).

The person P carrying the pole would conclude the length AB  of the barn is only $\rm{L}/\gamma$ and so when the front end Y touches the backend X would be outside and so the door cannot be closed. The resolution of the paradox  occurs when you solve the next two problems.

46. How do the set of events appear from the two frames: (a) Y touches the wall AE. (b) the door closed at the time the pole touches AE as seen by the person at rest with respect to the barn (c) the position of X when Y touches the wall.

47. Let us now analyse using the pole's frame where the door  and the barn are are moving with a velocity -V. Assume that when the front end of the pole touches the wall AE a signal is sent to the door with a speed equal to the velocity of light to stop suddenly. When does the signal reach the door? Where will the door be when the signal reaches it?

Now write a small note (please be brief !) on the resolution of the paradox.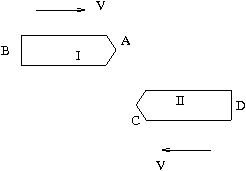



48. Spaceship warfare: Two spaceships AB and CD of equal rest length L are travelling along the $x_1$ axis in opposite directions with a relative velocity V. When the pilot A crosses the end D of  ship II she fires a missile from B downwards , thinking the missile will miss the ship as it has only length $L/\gamma$. However according to II it is the ship I which has a length $L/\gamma$ and so will hit the ship. What actually happens ? Analyse the two events in both the frames and describe it from both frames. You must give the coordinates of A,B,C,D for the events from both the frames.

49 . We had derived the Doppler shift formula
\begin{equation}
 \nu_{moving}\ =\  (\frac{1+\frac{v}{c}}{1-\frac{v}{c}})^{1/2}\, \nu_{rest}
\end{equation}
for the case when the source was moving  with a velocity $v$ towards the detector and the detector is at rest. Derive the same formula when the detector is moving towards a source which is at rest. (The two answers should be the same as this depends only on the relative velocity between the source and the detector)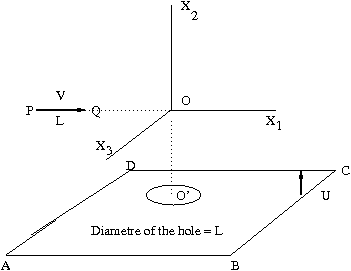



50. Plane and a space ship:  Consider a space ship of rest length L. The statements given below are from the frame(S)  at rest weith respect to origin O . The spaceship is approching the origin O from negative $x_1$ axis  with a velocity V$\hat{\epsilon}_1$. and the centre of the ship will reach the origin at t = 0. There is a sheet of steel, parallel to the $x_1-x_3$ plane  with a hole of diametre L moving up along $\hat{\epsilon}_2$ and O'. The centre of the hole O' reaches O at t=0.

According to the ship's rest frame the hole will appear to be elliptical with contraction along $X_1$ axis and the pilot will conclude that the plane will crash on the steel sheet.

According to an oberver in S the plane will look contracted and pass through the hole.

What actually happens?