[XMP/QM-13001] Short Examples --- Nature of Energy Spectrum

The nature of energy spectrum can be classified into three following classes.

• [Class 1] Discrete energy levels
• [Class 2] Continuous and doubly degenerate levels
• [Class 3]Continuous and non degenerate levels

We will two give examples each of potentials with specified energy levels of specified classes. is described.

1. Potentials having only class 1 levels: 
Harmonic oscillator and Infinite well
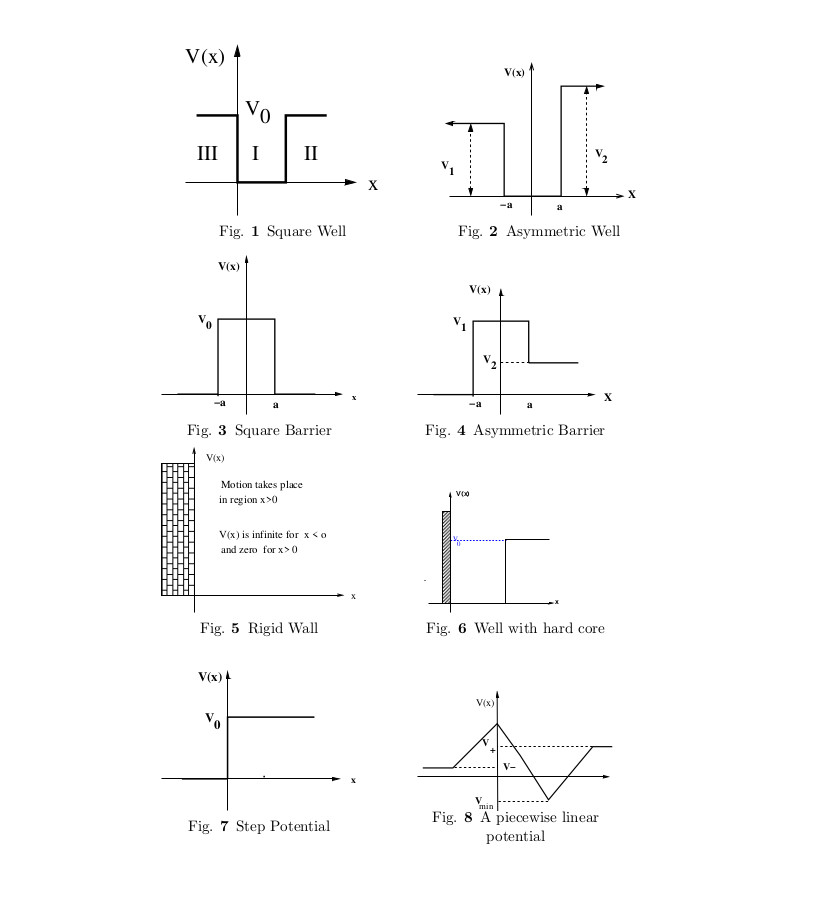
2. Potentials having only class 2 levels:
Square barrier, Fig. 3. and \(V(x)= g\, \sech^2 \alpha x, g>0\),
3. Potentials having only class 3 energy states:   
The exponential potential \(V(x)= g e^{\alpha x}, \alpha >0, g>0\) and Rigid wall at \(x=0\)
4. Potentials having class 1 and class 2 levels, but not having class 3 levels:
Square well, Fig. 1 and \(V(x)=-g\, \sech^2\alpha x , g>0\)
5. Potentials having class 1 and class 3 levels, but not of class 2:
Square well with a hard core, Fig. 6 and Morse potential, \(V(x) =A (e^{-2ax}-2e^{-ax}) \)
6. Potentials having class 2 and class 3 levels but with no class 1 level:
Step potential ,  Fig. 7 and Asymmetric barrier, Fig. 4
7. Potential having all three types of states: 
Two examples are sketched in Fig. 2 and Fig 8.