Category:
The definition of cross section is formulated in probabilistic terms. This interpretation turns out to be useful for interpretation of the cross section as an area, and also for quantum mechanical problems.
For scattering of waves the cross section corresponds to an area of the wave front. What is the interpretation of the cross section for a beam of particles? Does it correspond to some area of cross section of the incident beam? What if the incident beam intensity is very low. So that at one time only one particle is incident?
In our discussion so far we have assumed an incident beam on a single scattering centre. Assume now that the target in the shape of a foil with lots of scatterers. Also assume that each scatterer acts independently of others so that the cross section can be obtained by summing over all individual scatterers.
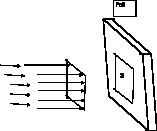
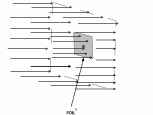
Let $S$ be the area of cross section of the beam as in Fig. 1, or that of foil as in Fig. 2, which ever is less.
 |
 |
|
| Fig 1 The foil area is more than the beam cross section | Fig . 2 Beam cross section is more than the foil area |
| Total number of particles removed from the beam in time $T$ | |
| $=$ no of particles removed in time $T$ by one scatterer $\times$ no.of scattering centres taking part in scattering . |
|
| $=\text{ (Number of particles removed by one centre in time \(T\)) }\times N \times S $ ....(A). | |
By definition of $\sigma_t$, we have no.of particles removed from the beam by one centre in time $ T=\sigma_t\times \text{Flux} \times T.$
Hence the right hand side of (A) is
$$\text{R.H.S.of (A)}=\sigma_t\times \text{Flux} \times t\times N\times S\dots \qquad\qquad \ldots (B)$$
Therefore from (A) and (B) we get
\begin{eqnarray} \sigma_t
&=&\frac{(\text{Total number of particles scattered by the foil in time } T)} {\text{Flux}\times S\times N \times T}. \\ &=&\frac{(\text{Total number of particles scattered by the foil in time } T)} {(\text{No.of particles incident on the foil in time } T) \times N }\\
&=&\frac{1}{N} \times \text{Probability of scattering from the foil}\\ \end{eqnarray}
In other words $\sigma_t$ is the probability that scattering takes place when there is one scattering center per unit area.






 ||Message]
||Message]
