[TALK/CM-06002] Let's Talk --- Potential Scattering

The potential scattering can be thought of as a limiting case of two particle scattering when the target is very heavy compared to the incident particle. In this case motion of the target can be ignored. The motion of the incident particle is taken as that of particle getting scattered from a potential created by the target.

As an another view, scattering of a two particle in the centre of mass frame of reference is same as the the potential scattering of a particle having mass equal to the reduced mass.

To discuss the scattering of a particle from a spherically symmetric potential $V(r)$, one works with plane polar coordinates. The position of the target is chosen as the origin, and the direction of the incident beam as the direction \(\theta =0\). Further we assume that the potential goes to zero at large distances.

The conservation of energy \(E\) and momentum conservation \(L\) fix the trajectory completely.
Knowing the potential, one can find the orbit and hence the position $\vec{r}\equiv\vec{r}(t)$ as a function of time is known.

For large times, $t\longrightarrow \pm\infty$, the particle is at large distances from the scattering center and moves like a free particle. At large distances its velocity remains constant. Thus in distant past and distant future the particle moves in a straight line.

The position vector, $\vec{r}(t)$, varies linearly with time $t$. The particles in the beam travels in a straight line in distant past and future.

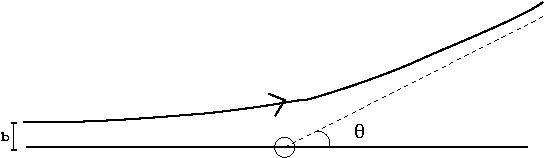
To define the scattering angle of a particle, we draw asymptotes to its trajectory at \(t=-\infty\) and at \(t=+\infty\). \\[3mm]

In case of a spherically symmetric potential, the angular  momentum \(L\) and the energy \(E\) are constants of motion and fully determine the trajectory. Hence the scattering angle \(\theta\) can be found as a function of \(E,L\).  Also the impact parameter is related to the angular momentum by \(\ell=mvb\), where \(v\) is the velocity of the particle at \(t=\pm \infty\). It is related to the energy by \(v=\sqrt{2mE}\). Thus we can find the scattering angle as a function of \(b,E\). Knowledge of this relationship,\(b\equiv b(E,\theta)\), is sufficient to determine the cross section in classical mechanics.