[NOTES/CM-06003] Particles --- Which area is the cross section?

To interpret the cross section let us assign an " Effective area (A) " to each scattering center. The foil can then be pictured as follows

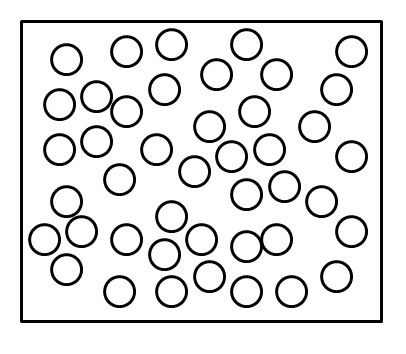
The probability that a particle gets scattered is given by

\begin{eqnarray}
&&\frac{\text{Total "area" presented by the scatterer}}
{\text{Area participating in scattering}}\\
&\qquad =& A \times \frac{\text{Total no.of scattering centres in area}
S}{S} \\
&\qquad=&\frac{A\times N\times S}{S}=AN \label{EQ02}
\end{eqnarray}

Recall that the total cross section for particle scattering can be written as
\begin{equation}\label{EQ03} \sigma_t=\frac{\text{Probability that a particle gets scattered}}
{\text{No.of scattering centres per unit area}}\end{equation}
Substituting for the numerator in the above equation, \eqref{EQ03}, from \eqref{EQ02} we get $\sigma_t=A$. Thus the total scattering cross section is the "effective area" presented by a scattering center to the incident beam.