Trying TOC Scattering Theory --- Basic Definitions

Scattering of Particles

We shall discuss elastic scattering \( a+b \Longrightarrow a+b \) of two particles interacting via a {\underline{central potential.}} We shall assume that the potential $V(\bf r)$ is spherically symmetric and goes to zero for large $r$ (How fast? faster than $\frac{1}{r^2}$).

If the forces are central,the scattering,two body problem, in the center of mass frame is equivalent to one particle motion in potential $V(\bf r)$, if we take the mass of the particle in the equivalent problem to be the reduced mass $\mu$. It is therefore sufficient to consider potential scattering.

Since the potential goes to zero for large distances, the total energy before and after scattering is $K.E.\simeq$ total energy. Thus the velocity before and after scattering, when the particle is for removed from the scattering center, is given by \(v\approx\sqrt{\frac{2 E}{\mu}}\).

Scattering Angle 

Experimentally, the scattering angle is the angle between the incident and the scattered beams.

Knowing the potential $V(r)$, one can find the orbit and hence the position $\vec{r}\equiv\vec{r}(t)$ as a function of time is known, For large times, $t\longrightarrow \pm\infty$, $\vec{r}(t)$ varies linearly with time $t$, if the effect of potential in distant past and distant future can be neglected. The particles travel radially outwards in a straight line. We draw asymptotes to the particle trajectory at \(t=-\infty\) and at \(t=+\infty\). Theoretically, the scattering angle is defined to be the angle between these asymptotes, see figure below.

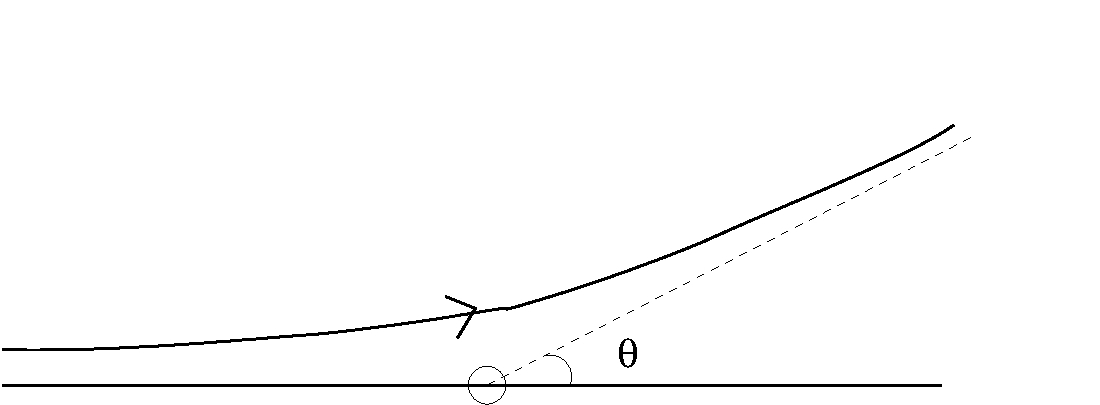
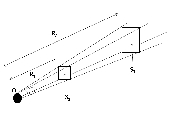
Solid angle of a detector

Consider two detectors placed at distances $R_1$ and $R_2$ but having (subtending) the same solid angle at the scattering center $O$, see \Figref{Scattering1}. Since the particles are moving radially outwards and are moving like free particles, they do not accelerate or 'crowd' in the region between the surfaces $S_1$ and $S_2$. As no particles are absorbed or created, the number of particles crossing $S_1$ per second will be equal to the number of particles crossing $S_2$ per second. Note that the two surface $S_1$ and $S_2$ correspond to the same solid angle \(d\Omega=\sin\theta \, d\theta \, d\phi\). As area of a surface at a distance $R$ is $d\Omega\times R^2$ will increases as $R^2$ with distance, the intensity, defined as %
\[ \boxed{\text{intensity=no of particles detected per sec per unit area}},\]
will fall like $\frac{1}{R^2}$ with distance $R$.

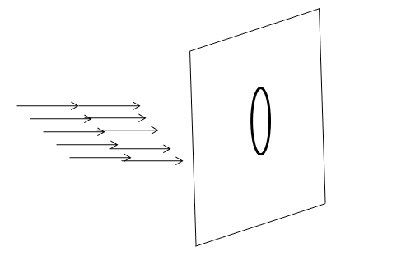
Flux

The flux of a beam is defined as number of particles in the incident beam crossing a unit area.(held perpendicular to the beam) per second.

Cross Section 

If the flux of the incident beam is increased the number of particles scattered will increase proportionately in every direction.

The constant of proportionality $\sigma_t$ is called the
Total cross section. Thus
\begin{equation}
\sigma_t\stackrel{\rm def}{\equiv} \frac{\text{Total no. of particles
removed from the beam per sec.}}{\text{Flux of the incident
beam.}}
\end{equation}
Similarly, we consider particles scattering in a given direction ($\theta,\phi$) into a solid angle $d\Omega$. Then the number of particles scattered into the solid angle $d\Omega$ will be proportional to the solid angle and to the incident flux. Thus we write
\begin{eqnarray}\text{No of particles}\hspace{-4mm}&&\hspace{-4mm}\text{removed from the beam and scattered}\\ && \hspace{-4mm}\text{ into the solid angle angle } d\Omega \text{ per sec}\\
&=&\sigma(\theta,\phi)\times \text{Flux} \times d\Omega
\end{eqnarray}
Therefore \(\sigma({\theta,\phi})d\Omega\) equals

\begin{eqnarray}
\frac{\text{No. of particles scattered per sec
into solid angle } d\Omega \text{ in }(\theta,\phi) \
\text{direction}}{\text{Incident Flux}}
\end{eqnarray}
Hence the differential cross section is given by
\begin{eqnarray}
\sigma({\theta,\phi})
=\frac{\text{No. of particles scattered per sec
per unit solid angle}}{\text{Incident Flux}}
\end{eqnarray}
Obviously integrating $\sigma({\theta,\phi})$ over all solid angles must give
the total cross section $\Omega_t$
\begin{equation}
\sigma_t
=\int\sigma({\theta,\phi}) \, d\Omega
=\int_{0}^{2\pi}d\phi\int_{0}^{\pi}\sin\theta \, \sigma(\theta,\phi) \,
d\theta
\end{equation}

Remarks

1. $\sigma(\theta,\phi)$ and $\sigma_t$ have dimensions of area \begin{equation} \sigma_t=\frac{\text{no. of particles/sec}}{\text{no. of particles/sec/area}}\sim \text{area} \end{equation} 
2. The expression $\frac{d\sigma}{d\Omega}$ is also used to denote the differential cross section $\sigma(\theta,\phi)$
3. It must be emphasised again that the numerator of definition of $\sigma(\theta,\phi)$ has the number of particles per unit solid angle and not per unit area. If it had per unit area, the "cross section" value $\sigma(\theta,\phi)$ would depend on $R$ the distance between the target and the detector.