[NOTES/QM-12002] Free Particle Wave Packets

Localization in quantum mechanics
A classical particle can have precise values of position and of momentum. On the other hand a wave is can have very precise value of wavelength, but it is not localized in space.
A quantum particle, due its dual nature, cannot have 100\% precise values of position and momentum simultaneously. Any attempt to make position well defined results in large uncertainty in momentum and vice-versa. It is therefore natural to ask, ``How are then particles represented in quantum mechanics?'' Consider a particle with a definite value of momentum $p$. It will be described by a plane wave:

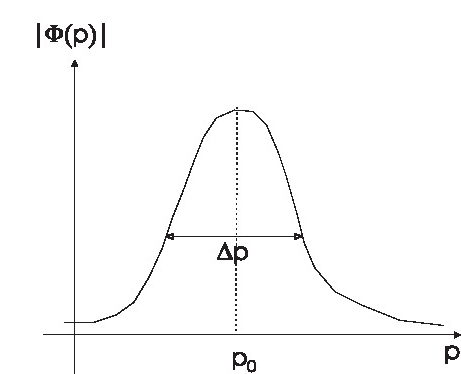
\begin{equation}\label{eq01} \psi(x) = e^{ipx/\hbar} \end{equation} and the probability density is $|\psi(x)|^2=1$ for all positions. Such a quantum particle has equal probability of being anywhere in space and is therefore not localised. However, if we form a superposition of states corresponding to a range of momenta values and consider the state given by the wave function of form \begin{equation}\label{eq02} \Psi(x) = \int_{-\infty} ^\infty \phi(p) e^{ipx/\hbar}\, dp, \end{equation} it is possible to describe a localized particle with a suitable choice of function \(\phi(p)\). A suitable choice of the function $\phi(p)$ is the one which has a maximum at some momentum value $p_0$ and has small value for momentum outside a range $\Delta p$ around $p_0$. One such function is shown in figure below. The Fourier transform $\psi(x)$ will be a function peaked around some point $x_0$ and will be appreciable within a range $\Delta x$ around $x_0$, schematically shown in see Fig.1 and  Fig,2 

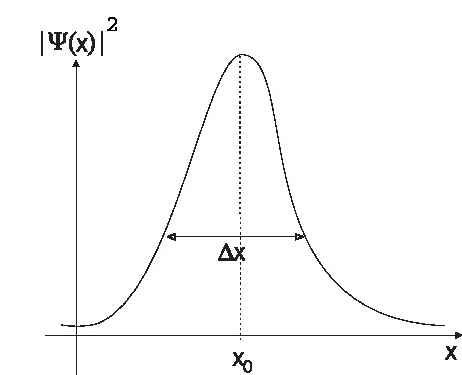Fig 1 $ |\phi(p)|^2$	Fig 2   $|\psi(x)|^2$

Note that $|\psi(x)|^2, |\phi(p)|^2$ give the probability densities for position and momenta of the quantum particle. Such a superposition represents a quantum particle localised in space around position $x_0$ and having uncertainty in position equal to $\Delta x$. The value $p_0$ gives approximately the value of average momentum of the particle. The spreads in the position and momentum will be constrained by the uncertainty relation $\Delta x\Delta p \ge \frac{\hbar}{2}$. Such a superposition of plane wave is called a {\bf wave packet}. A wave packet is a close representation of classical particle having definite position and momentum values. 

Several questions need to be answered at this stage. How can we locate the position of the peak ? What happens as time passes? Does the time evolution of a wave packet in any way resemble the motion of a free particle? To answer these questions we take up an example of a very special wave packet known as {\it Gaussian wave packet}.

Time evolution of a Gaussian wave packet
 Gaussian wave packet is described by the following wave function. \begin{equation}\label{eq03} \psi(x) = (2\pi\Delta^2)^{-\frac{1}{4}} \exp\Big(-(x-x_0)^2/ 4\Delta^2 + i p_0x/\hbar \Big). \end{equation} For such a wave function we have \begin{eqnarray}\label{eq04} \langle x\rangle &=& \int_{-\infty}^{\infty} \psi^*(x) x \psi(x) \, dx = x_0 \\ \langle p \rangle &=& \int_{-\infty}^{\infty} \psi^*(x)\Big(-i\hbar \dd{x}\Big) \psi(x) \, dx\label{eq05}\\ (\Delta x)^2 &=& \langle x\rangle^2 -x_0^2 =\left( \int_{-\infty}^{\infty} \psi^*(x) x^2 \psi(x) \, dx\right)- x_0^2 = \Delta ^2\label{eq06} \\ (\Delta p)^2 &=& \langle p\rangle^2 -p_0^2 = \left(\int_{-\infty}^{\infty} \psi^*(x) \Big(-\hbar^2 \DD{x}\Big) \psi(x) \, dx\right) - p_0^2 = \hbar^2\Delta ^2. \label{eq07} \end{eqnarray} The above wave packet represents a particle localised around $x_0$ and having average momentum $p_0$. We will now obtain the time evolution of a Gaussian wave packet and demonstrate explicitly that the time development of the wave packet closely follows the motion of a classical particle. \subsection{Motion of a free particle wave packet} Given the wave function \eqref{\labelPrefix;eq03} as wave function at time $t=0$, and taking the Hamiltonian as the free particle Hamiltonian, how does the wave packet move? This can be answered by finding its wave function at time $t$ following the steps given below.

1. Find the eigenfunctions of the Hamiltonian, and for a free particle these are given by plane waves \begin{equation}\label{eq08} \psi_p(x) = e^{ipx/\hbar}. \end{equation}
2. Write the wave function at time $t=0$ as superposition of the energy eigenfunctions: \begin{equation}\label{eq09} \psi(x) = \int_{-\infty}^\infty \phi(p) e^{ipx/\hbar}\, dp \end{equation} where the superposition coefficients \(\phi(p)\) are given by \begin{equation}\label{eq10} \phi(p) = \left(\frac{1}{2\pi\hbar} \right) \int_{-\infty}^\infty \psi(x) e^{-ipx/\hbar}. \end{equation}
3. The wave function $\Psi(x,t)$, at time $t$, is obtained by supplying a factor $\exp(-iEt/\hbar)$ with the plane wave inside the integral in \eqref{eq09}. \begin{equation}\label{eq11} \Psi(x,t) = \int_{-\infty}^\infty \phi(p) e^{ipx/\hbar} e^{-iE_pt/\hbar} \, dp. \end{equation} In the present case of free particle, $E_p=\frac{p^2}{2m}$.
4. Computing $\phi(p)$ from \eqref{eq10} and substituting in \eqref{eq11} and doing the $p$ integral gives the wave function at time $t$\begin{eqnarray}\nonumber \Psi(x,t) &=& (2\pi\Delta^2)^{-1/4}\left( 1+ \frac{i\hbar t}{2\Delta^2 m}\right) \\&& \qquad \qquad \times \exp\left[- \frac{1}{1+ i\hbar t/2\Delta^2 m} \left\{- \frac{x^2}{4\Delta^2} + \frac{ip_0x}{\hbar} - \frac{ip_0^2t}{2m\hbar} \right\} \right] \label{eq12} \end{eqnarray} The position probability density is given by \begin{eqnarray}\label{eq13} |\Psi(x,t)|^2 = (2\pi\Delta^2)^{-1/4} \left( 1+ \frac{i\hbar ^2 t^2}{2\Delta^2 m}\right) \exp\left[- \frac{x^2}{4\Delta^2 (1+\frac{\hbar^2 t^2}{(1+4 m^2 \Delta^2)} }\right]. \end{eqnarray}
5. The average value of momentum and the uncertainty in momentum are given by \begin{equation} \langle p \rangle_t= p_0, \qquad \qquad \end{equation} The average position at time $t$, and the uncertainty in position at time $t$ are given by \begin{eqnarray}\label{eq14} \langle x \rangle_t &=& \int_{-\infty}^\infty \Psi^*(x,t) x \Psi(x,t) dx,\\ &=& x_0 + \frac{p_0t}{m} = x_0 + vt \label{eq15}\\ (\Delta x)_ t &=& (\Delta x)_0\left(1+ \frac{\hbar^2t^2}{4\Delta^2m^2} \right)^{1/2}.\label{eq16} \end{eqnarray}

The average position changes with time as expected from the classical free particle motion. Also, remembering that the spread in position at time $t$ is $(\Delta x)_t$, we see that the uncertainty in position increases with time. Thus there is a spreading of the wave packet with time. The spreading takes place because the wave packet is a superposition of plane waves and different waves have different velocities.