[YMP/EM-03005] Electric potential due to a thin spherical shell

Let a point \(P\) be at a distance \(r\) from the center of the spherical shell;
Consider a ring shaped surface of the shell between \(x\) and \(x+dx\) 
Radius of the sphere = \(a\)
Radius of the ring =$a\sin\theta$
$x=a\cos\theta$
Area of the ring =$(ad\theta)\times(a\sin\theta)\times 2\pi$
$dx=a\sec^2\theta d\theta$
charge density $\sigma =\frac{Q}{4\pi a^2}$

\begin{eqnarray}
d\phi&=&(\frac{1}{4\pi\epsilon_0})\frac{\sigma 2\pi a^2 \sin\theta d\theta}{R}\\\label{eq25}\nonumber
&=&(\frac{1}{4\pi\epsilon_0})\frac{Q}{2}\frac{\sin\theta
d\theta}{\sqrt{r^2+a^2-2ar\cos\theta}}\\
\nonumber&=&(\frac{1}{4\pi\epsilon_0})\frac{Q}{2}\int_0^{\pi}\frac{\sin\theta
d\theta}{\sqrt{r^2+a^2-2ar\cos\theta}}\\
\nonumber
\therefore \quad \phi &=&\frac{Q}{8\pi\epsilon_0}\int_0^{\pi}\frac{dt}{\sqrt{r^2+a^2-2art}}\\
\nonumber&=&\frac{-Q}{8\pi\epsilon_0ar}[\sqrt{r^2+a^2-2art}\Big|_{t=-1}^{t=1}\nonumber\\
&=&\frac{Q}{8\pi\epsilon_0ar}[((r+a)^2)^{1/2}-((r-a)^2)^{1/2}] \label{eq26}
\end{eqnarray}

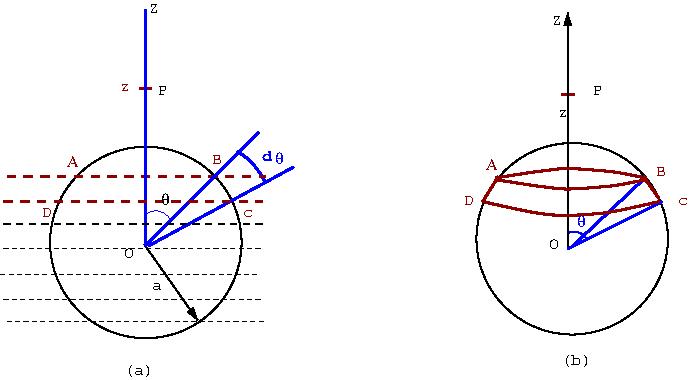Fig 1.  Dividing the spherical surface into ribbons of width \(d\theta\)

In \eqref{eq26}, one needs to be careful about the square root; the positive value of the square root should be used. Thus
\begin{equation}
((r-a)^2)^{1/2} = |r-a|
= \begin{cases}
r-a, & \text{if } r >a \\
a-r, & \text{if } a >r.
\end{cases}
\end{equation}
Therefore, we get
\begin{equation}
\phi(r)=
\begin{cases}
\dfrac{Q}{8\pi\epsilon_0 ar}(2a)
=\dfrac{Q}{4\pi\epsilon_0 r}, & r > a\\[3mm]
\dfrac{Q}{8\pi\epsilon_0 ar}(2r)
=\dfrac{Q}{4\pi\epsilon_0 a} & r < a,
\end{cases}
\end{equation}