[YMP/EM-03008] Field due to a Uniformly Charged Ring

The electric potential, $\phi$, due to a uniformly charged ring (radius \(a\) ) with charge density $\lambda$ at a point just above the center at a distance \(z\) is:

\begin{eqnarray}
d\phi&=&\frac{1}{4\pi\epsilon_0}\frac{(a d\theta)\lambda}{\sqrt{a^2+z^2}}\\\label{eq20}
\nonumber\phi
&=&\frac{1}{4\pi\epsilon_0}\int_0^{2\pi}\frac{ a \lambda\, d\theta}{\sqrt{a^2+z^2}}\\
&=&\frac{1}{4\pi\epsilon_0} \frac{Q}{\sqrt{a^2+z^2}}\label{eq21}
\end{eqnarray}

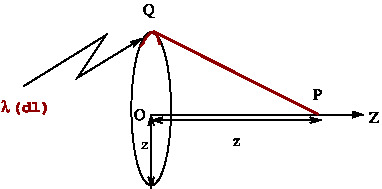
where \(Q =2\pi a \lambda\) is the total charge on the ring. For large \(z\) the potential becomes
\begin{equation}
\phi \approx \frac{Q}{4\pi\epsilon_0 z}
\end{equation}