Solved Examples --- Computation of Electric Field
- Electric Field due to a Uniformly Charged Disk
- Electric Field of a Uniformly Charged Spherical Shell
- Field due to a Uniformly Charged Ring
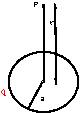
[YMP/EM-02006] Electric Field due to a Uniformly Charged DiskNode id: 6019We will show that the electric field due to a uniformly charged disk at a point on the axis of the disk is given by
|
||
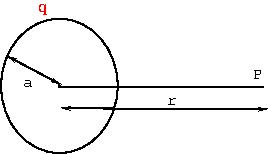
[YMP/EM-02007] Electric Field of a Uniformly Charged Spherical ShellNode id: 6020We will show that for a uniformly charged sphere, radius \(a\) and charge \(Q\),
|
||
|
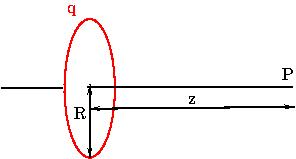
[YMP/EM-02005] Field due to a Uniformly Charged Ring Node id: 6018The electric field due to a charged ring, at a point, \(P\) on its axis, is computed using Coulomb's law. We will show that the electric field of uniformly charged ring, radius \(R\), at a point on the axis of the ring, is given by
|






 ||Message]
||Message]