Using Stokes theorem and Maxwell's equation \(\text{curl} \vec E =0\) it is proved that the tangential component of the electric field vanishes outside, just near the surface, vanishes.
A property of an ideal conductor in static situations is that the tangential component of the electric field vanishes near the surface of the conductor. This result will be proved using \(\text{curl} \vec E =0\) and Stokes theorem.
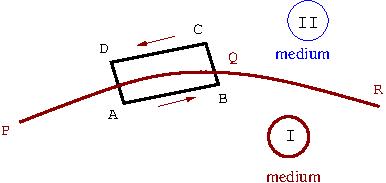 |
In Fig. 1, we have shown a surface \(PQR\) as a boundary separating two media I and II. We draw a rectangle \(ABCD\) with sides \(AB\) and \(CD\) parallel to the tangent to the surface. Integrating \(\text{curl} \vec E=0\) over the area of the rectangle \(ABCD\) we get \begin{equation} \iint_{ABCDA} (\text{curl} \vec E\cdot\hat n) dS =0. \end{equation} |
| Fig 1 |
Using Stokes theorem we get \begin{equation}\label{EQ06}
\left \{\int_{AB} + \int_{BC} + \int_{CD}
+\int_{DA} \right\} \vec E \cdot \overrightarrow{d\ell}=0
\end{equation} Next, a limit is taken in which the length of the sides \(BC\) and \(DA\) tends to zero. In this limit the second and the fourth terms in \eqRef{EQ06} vanish and \begin{eqnarray} \int_{AB} \vec E \cdot \overrightarrow{d\ell} + \int_{CD} \vec E\cdot \overrightarrow{d\ell}=0\\
\text{ or } \int_{AB} \vec E \cdot\overrightarrow{d\ell}- \int_{DC} \vec E \cdot \overrightarrow{d\ell}=0 \end{eqnarray}
Let \(\vec E_1\) and \(\vec E_2\) denote the electric field in regions I and II, and \(\hat t\) denote the unit tangent vector having direction same as \(\overrightarrow{AB}\). Then we have
\begin{eqnarray}
\int_{AB}\big(\vec E_1-\vec E_2\big) \cdot \hat t\, d\ell=0
\end{eqnarray}
If the sides \(AB\) and \(DC\) are taken as infinitesimally small, say \(d\ell\), we get
\begin{eqnarray}
\big(\vec E_1-\vec E_2\big) \cdot \hat t =0
\end{eqnarray}
This equation means that the component of the electric field parallel to the boundary is continuous.\(E_1^{\parallel} =E_2^{\parallel}\).
With this general result proved, we can derive the result we set out to prove. We take medium I to be the body of a conductor, and the medium II to be the air. Recalling that the electric field inside the body of a conductor is zero, we arrive at the result that the parallel component of the electric field just outside the conducting surface vanishes.






 ||Message]
||Message]
