[NOTES/EM-04011] Systems of Several Conductors

Consider a  system of several conductors having charges\(Q_1, Q_2, \ldots\), charge densities \(\sigma_1, \sigma_2.\ldots.\). Let the potentials of the conductors be denoted by \(\phi_1, \phi_2,\ldots\). It can be proved that  the potentials are linear functions of the charges, i.e 
\begin{equation}\label{EQ01} \phi_j = \sum_{k} p_{jk} \phi_k. \end{equation}
where \(p_{jk}\) are constants that depend only on the geometry of the system. it can be shown that the coefficients are symmetric in two indices, \(p_{jk}=p_{kj}\). it may not always be possible to compute the coefficients \(P_{jk}\), but they can be measured experimentally. The \eqref{EQ01} can be inverted to write the charges in terms of potentials  i.e.
\begin{equation} Q_j = \sum_k C_{jk} \phi_k. \end{equation}
For a system consisting of only one conductor, such as a metallic sphere, the above relations reduce to relation between the potential and the charge on the conductor. Thus for example for a spherical conductor of radius \(R\) we have
\begin{equation} \phi= \frac{Q}{4\pi \epsilon_0 R}, \qquad p_1=\frac{1}{4\pi\epsilon_0 R}. \end{equation}
Example 1
A capacitor consisting of two conductors held at potentials \(\phi_1\phi_2\) is a system with charges \(Q, -Q\) on the conductors. The capacitance \(C\) of such a system is
\begin{equation} C =\frac{Q}{\phi_1-\phi_2}. \end{equation}
We will relate the capacitance \(C\) to the constants \(p_11, p_{12}=p_21, p_{22}\). We have
\begin{eqnarray} \phi_1 &=& p_{11} Q_1 + p_{12} Q_2 \\ \phi_2 &=& p_{21} Q_1 + p_{22} Q_2. \end{eqnarray}
and for a capacitor, we choose \(Q_1=-Q_2=Q\). Therefore,
\begin{equation} \phi_1 = (p_{11}-p_{12}) Q, \qquad \phi_2= (p_{21}-p_{22}) Q. \end{equation}
Subtracting these equations we get \begin{equation} \phi_2-\phi_1 = (p_{11}+p_{22} -2p_{12}) Q. \end{equation}
Hence the capacitance is given by
\begin{equation} \boxed{   C =\frac{1}{p_{11}+p_{22}-2p_{12}}}\label{EQ09} \end{equation}
Example 2
Next we take example of a spherical condenser consisting of two concentric conducting shells of radii \(R_1, R_2\)and show how the coefficients in relations \eqref{EQ01} and \eqref{EQ02} can be fixed. If the shell have charges \(Q_1, Q_2\) and potentials \(\phi_1,\phi_2\), then \
begin{eqnarray}\label{EQ41} \phi_1 &=& p_{11} Q_1 + p_{12} Q_2 \\ \phi_2 &=& p_21 Q_1 + p_{22} Q_2. \label{EQ42} \end{eqnarray}
We will consider special cases of values of charges on the shell and determine the constants \(p{11}, p_{12}, p_{22}\).
Special Case-I
We first take the charge on inner shell to be zero, \(Q_1=0 Q_2=Q\), then we have
\begin{equation} \phi_1=\phi_2= \frac{Q_2}{4\pi\epsilon_0}. \end{equation}
The equations \eqref{EQ41}, \eqref{EQ42} give
\begin{equation} p_{12}= p_{22} = \frac{1}{4\pi \epsilon_0}. \end{equation}
Special Case-II
We now take \(Q1=Q\) and \(Q_2=0\). In this case
\begin{equation} \phi_1 =\frac{Q}{4\pi\epsilon_0 R_1}, \qquad \phi_2 =\frac{Q}{4\pi\epsilon_0 R_1}. \end{equation}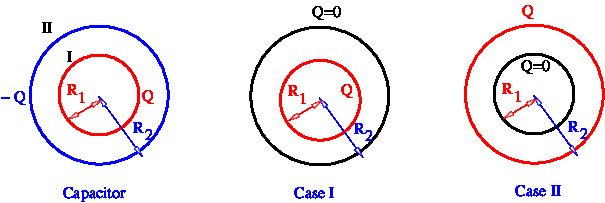



We now recall the result \eqref{EQ09}, of the previous example,
\begin{equation}q \frac{1}{C} = p_{11}+p_{22}-2p_{12}. \end{equation}
and substitute the values of \(p_11, p_{12}, p_{22}\), we obtain the expression of the capacitance of the spherical capacitor
\begin{equation} C = 4\pi\epsilon_0 \frac{R_1R_2}{R_2-R_1}. \end{equation}