[NOTES/EM-04001] Conductors in Electrostatics

A perfect conductor is modeled as  having electrons which are free to move inside the body of the conductors. Several properties of perfect conductors in presence of electrostatic field are discussed below. These properties do not hold when fields are changing with time.

• The electric field inside a conductor is zero.When a conductor is placed in an external electric field, the electrons  move freely in the direction opposite to the field. When they reach  the boundary, they cannot leave the conductors so they accumulate on the boundary. These charges set up their own, induced, electric     field and the induced field must add to give zero net electric field.

• $\rho=0$ inside the body of the conductor.This is because the electric field is zero inside a conductor and hence Maxwell's equation\begin{align}\label{eq001}    \nabla\cdot\vec{E} = \frac{\rho}{\epsilon_0}\end{align}implies $\rho=0$ inside the body of the conductor.
• Any net charge resides on the surface.This is a restatement of the fact that the charge density inside a conductor is zero.
• Electrostatic potential is constant throughout the conductor.Let us assume that the potential $\phi$ is not constant in the body of conductor. Then $\nabla\phi\ne0\Rightarrow\vec{E}(\vec{r}) \ne 0$ inside the conductor which is not possible. Hence $\phi=$constant. It can also be seen by noting that    \begin{align}\label{eq002}    \phi(b)-\phi(a) = - \int_a^b    \vec{E}(\vec{r})\cdot\overrightarrow{dl}\,\,,    \end{align}and we take path of integration from $a$ to $b$ inside the conductor. Since $\vec{E}=0$ we get $\phi(b)-\phi(a)=0$.

• $\vec{E}$ is perpendicular to the surface of the conductor.  Any non-zero component of the electric field along the tangent will make the charges flow along the surface which is ruled out in static situation.

• The electric field inside an empty cavity in a conductor is zero.A proof of this statement  follows from  the fact that the electrostatic forces are conservative. To prove that the electric field inside the empty cavity is zero, let us assume that the electric field can be non-zero and derive a contradiction. Let us consider the line integral of $\vec{E}$ along a closed path \(\Gamma\) consisting of $\Gamma_1$ along an electric line of force inside the cavity and $\Gamma_2$ in the body of conductor, see \Figref{em-fig-04009}.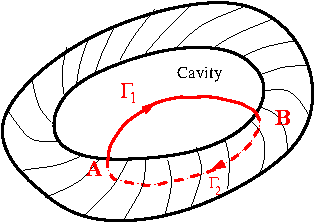Then \begin{align}\label{eq003} \int_{\Gamma_1}\vec{E}\cdot\overrightarrow{dl} + \int_{\Gamma_2} \vec{E}\cdot\overrightarrow{dl}=\int_{\Gamma_1}\vec{E}\cdot \overrightarrow{dl}~\ne~0 \end{align} The right-hand side is positive because $\Gamma_2$ runs parallel to the field and $\vec{E}\cdot\overrightarrow{dl}=\vec{E}\cdot\overrightarrow{dl}$ is positive all along the path $\Gamma_1$. To get a contradiction, we note that the conservative nature of electrical forces implies that the left-hand side being work done on a unit positive charge in a closed loop must vanish. Therefore \begin{align}\label{eq004} \int_{\Gamma_1}\vec{E}\cdot\overrightarrow{dl} + \int_{\Gamma_2}\vec{E}\cdot\overrightarrow{dl} = \oint_\Gamma \vec{E}\cdot\overrightarrow{dl}=0\,\,. \end{align} Hence the field inside an empty cavity must vanish.

• Induced charge inside the walls of the cavity. If the cavity is non-empty, and contains charge $q$, the total charge induced on the walls of the cavity will be $-q$. This result follows by applying Gauss's law to a closed surface inside the body of the conductor and enclosing the cavity. The electric field on  such a surface is zero and hence the flux through the surface must be zero. This implies that the net charge in the volume enclosed will be zero. Since the charge can only be on the surface, $-q$ is the total charge on the inner walls of the conductor surrounding the cavity. Induced charge inside the walls of the cavity.