[NOTES/EM-03016] Electric Potential of Finite Charged Line Segment

Consider a line  \(AB\) on which a uniform charge \(\lambda\) per unit length has been glued. We wish to compute the electric potential at a point \(P\),see Fig.1(a). We set up a coordinate system,  such that  the origin, \(O\) on the line \(AB\), \(X\)- along the line. For clarity, the axes are drawn separately in Fig 1(b).  The end points of the line charge are at \((a,0,0)\) and \((b,0,0)\).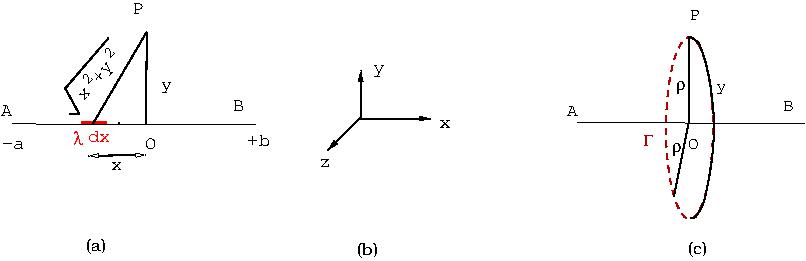

The contribution of a line element \(dx\) to the potential at the point \(P\) at a distance \(y\) from the line charge is
\begin{equation}
 d\phi = \frac{\lambda dx}{4\pi\epsilon_0}\frac{1}{\sqrt{x^2+y^2}}
\end{equation}
Therefore, the potential is given by
\begin{eqnarray}
 \phi &=& \int_{-a}^b\frac{\lambda dx}{4\pi\epsilon_0}\frac{1}{\sqrt{x^2+y^2}}\\
&=& \frac{\lambda}{4\pi\epsilon_0}
\int_{-a}^b \frac{dx}{\sqrt{y^2+x^2}}
\end{eqnarray}The last integration can  be carried out by changing variable to \(t\), using \(x=y\sinh t\) and using the  identity
\begin{eqnarray}  \sinh ^{-1} u = \ln (u + \sqrt{1+u^2}). \end{eqnarray}
We quote the final answer \begin{equation}
 \phi = \frac{\lambda}{4\pi\epsilon_0}
 \ln\left\{\frac{b^2+ \sqrt{y^2+b^2}}{a^2+\sqrt{y^2+a^2}} \right\}
\end{equation}Due to rotational symmetry about the line, the \(X\)-axis, the potential will be the same everywhere on the circle \(\Gamma\), with center at the origin and radius \(y\), see Fig.1(c).

Thus the potential at a distance \(\rho\) from the line charge is \begin{equation}
 \phi(\rho) =  \frac{\lambda}{4\pi\epsilon_0}
 \ln\left\{\frac{b^2+ \sqrt{\rho^2+b^2}}{a^2+\sqrt{\rho^2+a^2}} \right\}.
\end{equation}
Two limiting cases are of interest.

• In the limit the  point \(P\) is at a large distance,\(\rho >>a, b\), the potential tends to the expression \begin{equation}  \phi(\rho) \to \frac{Q}{4\pi \epsilon_0}\frac{1}{\rho} \end{equation}for a point charge \(Q\), where \(Q=\lambda(b-a)\) is the total charge on the line. This is expected intuitively, because a line charge from a large distance will appear as a point charge.

• For a line charge extending to infinity on both sides, taking \(a=-b, b\to \infty\), it is seen that the potential takes the form\begin{equation} \phi =\frac{\lambda}{4\pi \epsilon_0 \rho}.\end{equation}

The details of the above results are left as exercise for the reader.