[NOTES/EM-02013] Solid Angle

1. Angle subtended by a curve

How do you define an angle subtended by a curve \(C\) at a point \(P\)?
We know that length of a circular arc of radius \(R\) is $R\theta$. This can be used to  define angle subtended by a curve \(AB\)  at a point \(P\) as follows.
 The angle subtended by the curve at \(P\) is just the angle \(\theta\) between lines \(PA\) and \(PB\). However, this view cannot be extended to define solid angle.
We draw  a circle \(\Gamma\) with centre at \(P\).
Let \(\gamma\) be the arc of the circle cut by the lines \(PA\) and \(PB\) as shown in Fig1(a).
Then the angle \(\theta\), subtended by the curve, can also be defined as
\begin{eqnarray}
\theta=\frac{\text{length of the arc } \gamma}{\text{radius of } \Gamma}. \label{eq9}
\end{eqnarray}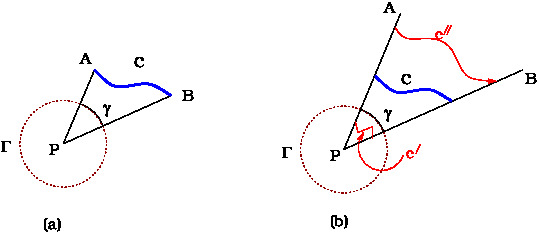

This definition can be extended to define solid angle subtended by a surface at a point \(P\).
From Fig/1(b) it is obvious that every other curve, such as \(C\Prime, C\prime\prime\) etc., with end points on the lines \(PA\) and \(PB\) subtends the same angle \(\theta\) at the point \(P\).

2. Solid angle subtended by a surface

We will now define the solid angle  subtended by a surface \(S\) at a point \(O\) in two different ways.

Definition 1
We draw a cone with O as the vertex and S as the base. We then find the area cut by the cone on a sphere of radius R with O as the centre. Then
\begin{eqnarray}
\text{solid angle}\stackrel    {\text{def}}{=}\frac{\text{area cut on the sphere}}{R^2} \label{eq10}
\end{eqnarray}


Definition 2

For a surface having infinitesimal area \(\Delta S\) located at \(\vec r\)
, the solid angle at a point \(O\) is
\begin{eqnarray}
 \Delta \Omega \stackrel{\text{def}}{=}
 \Big(\frac{\hat n \cdot \hat R}{R^2}\Big)
 \Delta S=\Big(\frac{\hat n \cdot (\vec r-\vec r_0)}{|\vec r-\vec r_0|^3}\Big)\Delta S\label{EQ03}
\end{eqnarray}
where \(\vec R= \vec r-\vec r_0\) and \(\hat n\) is the unit vector normal to the surface \(\Delta S\).

3. Solid angle for a finite surface


We have so far talked about the solid angle of an infinitesimal surface element.  By dividing a given surface into large number of elements, the solid angle of a finite surface subtended at a point \(\vec r_0\) can be written as a sum of expressions \eqRef{EQ03}. Thus
for a finite surface, the solid angle is  
defined as a surface integral
\begin{equation}\label{SolidAngle}
 \Omega_S = \iint_S \frac{\hat n \cdot (\vec r- \vec r_0)}{|\vec r- \vec r_0|^3}\, dS.
\end{equation}