[NOTES/EM-07002]-Current Conservation

Equation of Continuity

$$ \vec{j} = \vec{\rho}\cdot\vec{v} $$ Amount of charge crossing a unit area per second. Represent flow of charges by a vector $\vec{J}$ called current density. Take a small surface of area $\Delta S$ to $\vec{J}$ then $\vec{J}$ gives charge flowing through the surface per second $$ \vec{J}\cdot\hat{n}~\Delta S $$ Charge flowing through a surface per sec \begin{align*} =&\int_S\vec{J}\cdot\hat{n}~dS\\ =&\text{current through the surface $S$}\\ &(\equiv~I) \end{align*}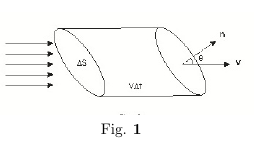

Let $V$ be a volume and $S$ be the surface enclosing the volume.\\ Charge flowing out of the closed surface $S$ per sec.\\ \(-\int_S\vec{J}\cdot\hat{n}~dS\)\\ \noindent Rate of decrease of total charge per second in the volume $$ = - \frac{d}{dt}~Q_m = -\,\frac{d}{dt}~\int_V \rho dV $$ $\therefore$~Charge conservation gives. $$ -~{d}{dt}\int \rho \,dV=\int_S\vec{J}\cdot\hat{n}~dS $$ or \begin{align*} \int_V\frac{\partial \rho}{\partial t}~dV + \int_S \vec{J}\cdot\hat{n}~dS&=0\\ or \int_V\left({\partial\rho}{\partial t}~+~\bar{\nabla}\cdot\bar{J}\right)dV &= 0\,. \qquad\qquad \text{for arbitrary $V$}\\ \frac{\partial\rho}{\partial V}~+~\vec{\nabla}\cdot\vec{J}&=0\,. \end{align*} The equation of continuity is a local form of conservation law in the sense that if charges is decreasing inside a volume $V$, it must be escaping through the surface. 
References

• Sec. 13-2 Electric current and conservation of charge R. P. Feynman, Robert B. Leighton and Mathew Sands{\it Lectures on Physics}, vol-II, B.I. Publications (1964)
• Sec. 8.1.1 The continuity equation David Griffiths, Introduction to Electrodynamics, 3rd EEE edn, Prentice Hall of India Pvt Ltd New Delhi, (2002).