[NOTES/ME-08004]-Sideways Deflection of a Freely Falling Body

We will discuss sideways deflection of a freely falling body. A body is dropped from height $h$ just above the point $P$, at time $t=0$ it will get a small deflection sideways and not reach ground at the point $P$. We will now calculate this sideways deflection. We begin with equation of motion in a rotating frame \begin{eqnarray}\label{EQ12A} \left.\DD[\vec{x}]{t}\right|_\text{rf} =\frac{\vec{F}}{m} - 2 \vec{\omega}\times \vec{v}- \vec{\omega}\times(\vec{\omega}\times\vec{x}). \end{eqnarray} The second term \(\omega^2\) will be neglected. The justification for this is as follows. Let \(t= \sqrt{2h/g}\) denote time of free fall from height \(h\). For \(h=100\text{\,m}, t\approx 4.5 \text{s}\), hence \(\omega t= \frac{2\pi}{24 \text{hrs}}\times t\) is very small and the second term can be neglected compared to the first term. \\ The equation of motion then takes the form \begin{eqnarray}\label{EQ12} \DD[\vec{x}]{t} \approx\vec{g} - 2 \vec{\omega}\times \vec{v} \end{eqnarray} where \(\vec{g}\) is the acceleration due to the earth's gravity. Choose the \(X_3\) vertically upwards, \(X_2\) axis towards north and \(X_1\) axis towards east.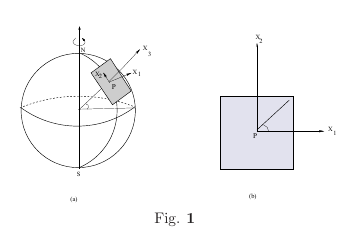 The earth's angular velocity has components \(\vec{\omega} = (0, \omega \cos\lambda, \omega \sin\lambda)\) where \(\lambda\) is the latitude of the place where the free fall is being observed. The acceleration due to earth's gravitational attraction is \(\vec{g}=(0,0,g)\). Then the $x_1$ component of equation of motion \EqRef{EQ12} takes the form \begin{equation} \DD[x_1]{t} = - 2 (\vec{\omega}\times\vec{v})_1= 2(\omega \cos\lambda) v_3- 2(\omega\sin\lambda) v_2 \approx 2 (\omega \cos\lambda) \,g t\label{EQ27} \end{equation} where we have used $v_3(t) = gt$ and dropped $v_2$ to write the last step in \EqRef{EQ27}. Integrating twice we get \begin{equation} \ddot{x}_1 = 2 g t(\sin\lambda) \Rightarrow \dot{x}_1 = gt^2 \cos\lambda \Rightarrow {x}_1 = \frac{gt^3}{3} \cos\lambda. \end{equation} Substituting the time taken to reach ground from a height $h$ as $t=\sqrt{\frac{2h}{g}}$, the expression for sideways deflection becomes \begin{equation} x_1 = \frac{g}{3} \left(\frac{2h}{g}\right)^{3/2}\omega \cos\lambda . \end{equation} Note that several approximations have been made to arrive at the above expression. For full details see \(\S\)30, Sommerfeld \cite{Sommer-Me}.