The Gauss law of electrostatics follows from the Coulomb’s law for a point charge and superposition principle. The proof given here follows Feynman’s lectures. It makes use of two important features of the electric field due to a point charge. These are
(i) the magnitude of the field obeying the inverse square law, and
(ii) radial direction of the electric field of a point charge. The above two properties are essential to the proof. Gauss law will not hold for hypothetical field, not having both the properties.
We shall follow Feynman and give a simple and direct proof of Gauss law for {\bf a single point charge}. The proof for an arbitrary charge distribution will then follow from superposition principle for the electric field.
Two properties of electric field of a point charge are important for this discussion. The first one is that the electric field is radial. The second property is the inverse square law for the magnitude of the electric field of a point
1. Flux through a small surface element
As a preparation for the proof, we first prove that the flux of the electric field of a point charge through certain surface elements are equal.
A special surface element
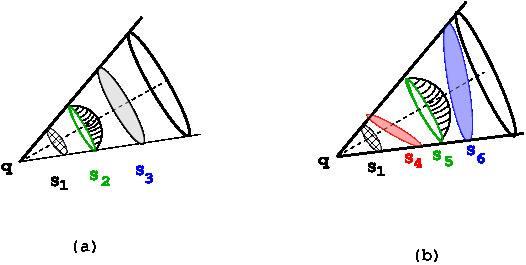
We start with the easiest case, consider a single point charge placed at the vertex of a cone with small solid angle. see Fig 1(a) and 1(b)
| In \Figref{em-fig-02021}(a), \(S_1\) is a part of a spherical surface of radius $R_1$ and has area $\Delta S_1$. \(S_2\) is a part of a spherical surface of radius $R_2$ and has area $\Delta S_2$ and so on. Then
\begin{eqnarray} \Delta S& \alpha& r^2 \label{eq1} \\ \frac{\Delta S_1}{R_1^2}&=&\frac{\Delta S_2}{R_2^2} \label{eq2} \end{eqnarray} Therefore, the outward flux through \(S_1\) is $ \Phi_{S_1}$ \begin{eqnarray} \nonumber\Phi_{S_1}&=&\mid\bar{E}\mid\Delta S \\ &=&\frac{q}{4\pi\epsilon_0}\frac{\Delta S_1}{R_1^2} \label{eq3}\\ \Phi_{S_2}&=&\frac{q}{4\pi\epsilon_0}\frac{\Delta S_2}{R_2^2} \label{eq4} \end{eqnarray} Using \eqref{eq2} in \eqref{eq4}, we get : \begin{eqnarray} \Phi_{S_1}&=&\Phi_{S_2} \label{eq5} \end{eqnarray} |
 |
| Fig 1 |
|
A tilted surface element \begin{eqnarray} \Delta S_4&=&\frac{\Delta S_1}{R_1^2} \frac{R_4^2}{\cos\theta}; \label{eq6} \end{eqnarray} Flux through \(S_4\) is $\Phi_{S_4}$ \begin{eqnarray} \Phi_{S_4}&=&\mid\bar{E}\mid\cos\theta\cdot\Delta S_4\label{eq7} \\&=&\frac{q}{4\pi\epsilon_0 R_4^2}\frac{\Delta S_1 R_4^2}{R_1^2}\label{eq8}\\ &=&\Phi_{S_1} \label{eq9A} \end{eqnarray} . |
 |
| Fig 2 |
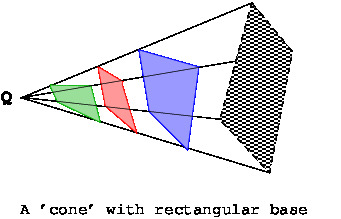
Note that \(S_1, S_2, S_3, S_4 ...\) must be very small so that $\mid\bar{E}\mid\cos\theta$ does not vary from place to place.\\ Thus we have seen that the flux of electric field of a point charge through two, or more small surface elements, remains equal if the boundary of the surfaces lie on the same cone with the vertex at the point charge position as in \Figref{em-fig-02021}(b). A similar statement holds for more general surfaces where the base of the cone is taken to be any curve. In examples shown in \Figref{em-fig-02022} we have a pyramid with a rectangular base and have shown several surfaces for which the flux of a point charge \(Q\) will be the same
2. An intuitive proof of Gauss Law
We will consider two cases separately. First we take up the case when a point charge is enclosed by the surface. The case of point charge lying outside the surface will be taken up next. The proof for general charge distribution is completed by appealing to the superposition principle for the electric field
The above sequence of steps proves the Gauss law for a point charge. The Gauss law for an arbitrary charge distribution follows from the superposition principle.
|
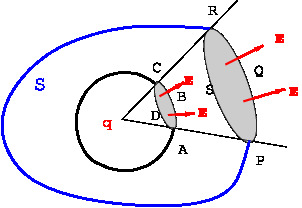
Case-I: Point charge enclosed by the surface Let us assume that the charge \(q\) is inside a closed surface \(S\). The position of the charge is taken as the origin of coordinate system. We draw a spherical surface with the point charge at the center such that the sphere is enclosed fully inside the surface. The given surface is divided into several infinitesimal elements. A cone is drawn with the charge at the vertex and a surface element \(PQRS\) as the base. This cone will cut a surface area \(ABCD\) on the spherical surface. The flux through the surface element \(PQRS\) on \(S\) and through \(ABCD\)on the sphere are equal. Summing over all the elements of the surface \(S\) we get the result that the flux through the given closed surface is equal to the flux through the sphere with center at \(q\) and the flux through the sphere has already shown to be, see Sec.\ref{PtChrgFlux} \begin{eqnarray} \Phi&=&q/\epsilon_0 \label{eq10A} \end{eqnarray} |
|
| Fig 3 |
| Case-II: Point charge not enclosed by the surface
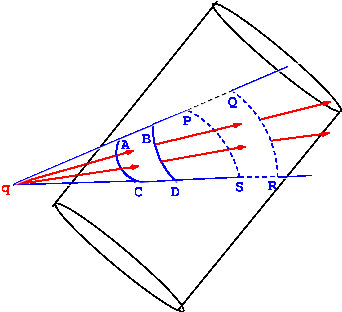
As an example of a closed surface we take a cylinder as shown in figure below. We divide the surface into large number of infinitesimal surface elements. One such element is \(PQRS\) shown in \Figref{em-fig-02023}. With the point charge as the vertex, a cone is drawn such that \(PQRS\) lies on the curved surface of the cone. This cone will intersect the closed surface in another infinitesimal element \(ABCD\). It can be seen that magnitudes of the flux through \(ABCD\) and \(PQRS\) are equal but opposite in sign. The signs are opposite because flux through \(ABCD\) will be inwards and the flux through \(PQRS\) will be outwards. Therefore, the net outward flux, through such pairs of surface elements vanishes. A closed surface can be divided into similar pairs of surface elements by cones in different directions. For each such pair the net outward flux of the field will be zero. Therefore the total flux is zero when charge \(q\) is outside. |
 |
| Fig 4 |
Reference
R. P. Feynman, Robert B. Leighton and Mathew Sands{\it Lectures on Physics}, vol-II, B.I. Publications (1964)
Exclude node summary :
Exclude node links:
4727:Diamond Point






 ||Message]
||Message]