Thermal Physics
Problem sheet 2
Each question carries 5 marks
28st September 2021
5th October 2021
Reading Assignment : From Hari dass's book example 2.5 ( A beautiful illustration of the application of thermal physics to atmosphere) You can actually verify ( or show the opposite) when you take a flight where there are height and temperature indicators. All interantional flights have this and some internal flights too. 4. Consider the following expressions for entropy. Which ones can possibly be a fundamental equation and which ones violate one or more of postulates II,III and IV?
(a) $$S\,=\,K_1\left(NVU\right)^{1/3}$$
(b) $$ S\,=\,K_2\left(\frac{NU}{V}\right)^{2/3} $$
(c) $$ S\,=\,K_3\frac{V^3}{NU}$$
(d) $$ S\,=\,N{\rm{\ln}}\left(\frac{UV}{N^2K_4}\right)$$
$K_i$'s are positive constants so that dimensions match. $S,U,N,V $ are the entropy, internal energy, number of particles and volume respectively.
5. Consider a closed cylinder whose walls are adiabatic. The cylinder is divided into three equal parts $A_1$, $A_2$ and $A_3$ by means of partitions $S_1$ and $S_2$, which can move along the length of the cylinder without friction. The partition $S_1$ is adiabatic and $S_2$ is conducting. Initially, each of the three parts contain one mole of Helium gas, which can be treated as an ideal gas, is at pressure $P_0$, temperature $T_0$ and volume $V_0$. Assume the specific heat at constant volume $C_v\,=\,\frac{3R}{2}$ and the specific heat at constant pressure $C_p\,=\,\frac{5R}{2}$. Now, heat is supplied to the to the left most partition $A_1$ till the temperature in part $A_3$ becomes $T_3\,=\,\frac{9T_0}{4}$ Find the final volume, pressure and temperature in terms of $V_0$, $P_0$ and $T_0$. Assume the entire process is quasistatic.
3. ( Continuation of problem 2)
(a) What is work done by the gas in $A_1$ ?
(b) What is the heat supplied to the gas in $A_1$? 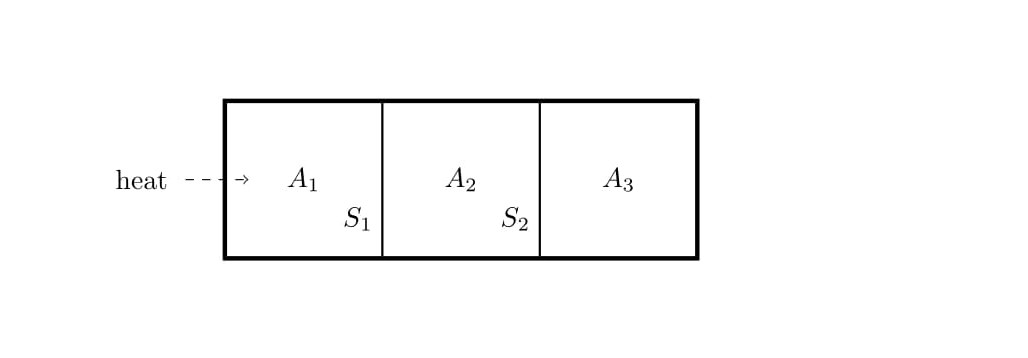
21th-hmw-02
For page specific messages
For page author info
n
0






 ||Message]
||Message]
