CMI CM-I Problem Sheet MidSem 2012

1. Find the conditions between $ L_1\, ,\, L,\, \rm{and}\, K $ ( see figure) for the oscillations about the vertical axis is stable.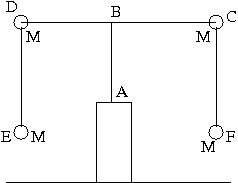



EDBCF is a rigid structure attached rigidly to the rod AB. The entire system is free to oscillate in the vertical plane about the axis perpendicular  to the paper passing through A. The angles between ED and DB, between DB and AB, between AB and BC, and between BC and CF are all $90^0$. Further $AB\, =\, K\,; DB\, =\, BC\, =\, L\, ; DE\,=\,CF\,=\, L_1$.

2. The potential between an atom ( infinitely heavy) and an ion ( mass m ) is given by $V(r)=-C/r^4\, ,\, C>0$ where $r$ is the distance between them. ( The atom is at $r=0$) The ion has an angular momentum $L$ with respect to the atom.

1. Draw the effective potential for the system.
2. Find the maximum value of the effective potential $V_0$ as a function of $L$.  
3. Draw the phase space trajectory in the space $(p_r ,r)\, r>0\,$ for values of the ion energy $E\, >\, V_0$ and $E\, <\, V_0$.

3. The orbit of a particle ( mass m) moving under the influence of a central force is $r\theta\,=\,\rm{constant}\, = K\, >0$.

1. Find the force law.
2. Find the potential.

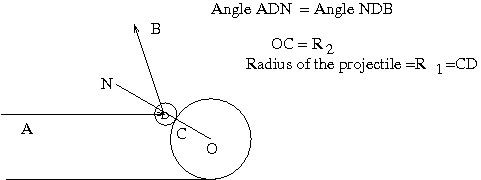
4. Find the differential cross section ($\frac{d\sigma}{d\Omega}$) and total cross section of the scattering of a spherical particle of mass m with radius $R_1$ with another spherical particle of infinite mass of radius $R_2$ and is at rest at the origin.  Treat the collision as elastic ( see figure).

5. A planet is going round the sun (infinite mass) with a speed $V_0$ when it is at its perihelion when its distance from the sun is $r_0$.

1. Find the eccentricity e of the orbit in terms of the Gravitational constant G, the speed $V_0$ and $r_0$.
2. Find the time it takes to complete one revolution in terms of G,$r_0\,\, \rm{and}\, V_0$.