CMI CM-I Problem Sheet 11 (2012)

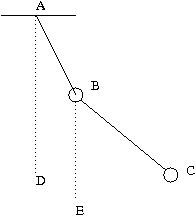
51. Consider the double pendulum shown in the figure. Masses of the two bobs at B and C is $m$. AB = $L_1$ BC = $L_2$ the angle DAB = $\theta_1$ and angle EDB = $\theta_2$ , where AD and BE are vertical. Write the Lagrangian and the equations of motion for the angles $\theta_1\, ,\, \theta_2 $. Write the Hamiltonian for the system.

52. Consider two equal masses A,B (M each) going around each other in a circular path of radius a about their centre of mass O with angular velocity $\omega\,= \, GM/(4a^3)$. A small satellite S of mass $m\, (\,m\, <<\, M\, )$ is moving under the influence of the two body system in the same plane as the orbits of A and B. Let (r,$\theta)$ represent the polar coordinates of S in the rotating frame in which A and B are rest with O as origin.  Write the Lagrangian for S  in terms of  (r,$ \theta$). Show that there are three points on the line joining AB ( and extended ) where the satellite is stationary (that is rotating along with the two body system). Find the points.

These points are known as Lagrange points $L_1,L_2,L_3$ - these are unstable. There are two more for which $\theta =90^0\,270^0$ - prove this-they are referred to as $L_4\,L_5$ and these are stable.Find the locations of $L_4,L_5$ (Stability analysis not required).
 
Note: There are similar points for the earth sun system ( we ofcourse had to redo the anaysis with appropriate masses). In fact WMAP a satellite is located at $L_2$ , a point located approximately at $1.5\,\times 10^6 k.m. $ from the earth. This is a satellite which measures the cosmic microwave background  anisotropy.

53. In the class I failed to make the point that one can commit a mistake if one is not careful about taking partial derivatives keeping in mind which variables are  held constant. Now the following problem illustrates this.

Consider a free particle whose Lagrangian $$L\,=\,T\,-\,V\,=\, T(q,\frac{dq}{dt})$$ We have the canonical momentum defined by  $$ p\ =\ \frac{\partial L}{\partial \frac{dq}{dt}} $$ thus using $$ \frac{d}{dt}\frac{\partial L}{\partial \frac{dq}{dt}}\ =\ \frac{\partial L}{\partial q}$$ we get
\begin{equation} \label{eq1}
 \frac{dp}{dt}\ =\ \frac{\partial T}{\partial q }
\end{equation}
Do a similar analysis for the Hamiltonian. $H\,=\, T\,+\,V\,=\, T$ and the Hamilton's equation of motion implies
\begin{equation} \label{eq2}
 \frac{dp}{dt}\ =\ -\frac{\partial H}{\partial q} = -\frac{\partial T}{\partial q}
\end{equation}
Equations (\ref{eq1}) and (\ref{eq2})  seems to imply $\frac{dp}{dt}\,=\,0$. However writing in terms of cylindrical coordinates $(r,\theta,z)$ the kinetic energy of a point particle of mass m is given by $T \,= \frac{1}{2}(m(\frac{dr}{dt})^2\,+\,mr^2\,(\frac{d\phi}{dt})^2\,+\,m(\frac{dz}{dt}^2) $ and $\frac{dp_r}{dt}\,\neq 0 $.
The problem is show this result in general. Consider a system with N degrees of freedom whose Lagrangian is $$ L(q_i,\frac{dq_i}{dt},t)\ =\ \frac{1}{2}\sum_{ij}^N F_{ij}(q)\frac{dq_i}{dt}\frac{dq_j}{dt} $$ where $F_{ij}\,=\,F_{ji}$. and are functions of N-independent co-ordinated $q_i$.The canonical momenta are given by $$ p_i\ =\ F_{ij}\frac{dq_j}{dt} $$
where  the summation convention has been used. Let $F^{-1}_{ij}F_{jk}\,=\, \delta{ik}$.
Show that $$ H(q_i,p_i,t) \ =\ \frac{1}{2}p_i(F^{-1})_{ij}p_j $$
Show that  $$ \frac{\partial H(q,p,t)}{\partial q} = -\frac{\partial L(q,\frac{dq}{dt},t)}{\partial q} $$ in spite of the fact $H\ = \ L \ =\ T$.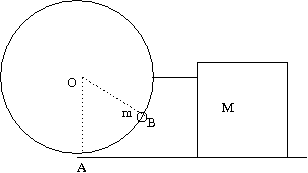


54. A block of mass M connected to massless ring of radius R by means of a massless rod. A bead of mass m is free to move slide on the ring. The motion is on a frictionless plane. Write the Lagrangian and the Hamiltonian of the system in terms of $x$ the coordinate of M and the  $\theta$ =  angle AOB. Find the equations of motion. In the limit of small $\theta$ find $\theta $ as a function of time.

55. Consider the relativistic motion of particle of rest mass m under the action of a constant force along $\hat{\epsilon}_1$. If the particle starts   at $t\,=\,0$ from the origin of an inertial frame S , find $x_1(t)$ and show its speed never exceeds that of light.