CMI CM-I Problem Sheet 8 (2012)

36. A projectile is fired vertically up with an initial velocity $\vec{U}_0\,=\,U_0\,\hat{\epsilon}_3 $ from a town located at latitude $\lambda$. Find the place it will come back to the ground taking the earths rotation into account. (East is along $\hat{\epsilon}_1$ and north along $\hat{\epsilon}_2$.

37. A merry-go-round starts from rest and constantly accelerates at $\alpha$ revolutions per second per second. a person is siting at a distance of $R$ metres from the axis of rotation and is holding a mass $M$ kilograms. Calculate the force (vector!)  the person must exert on the mass after time $t$. The person's co-ordinates at $t\,=\,0$ is $R\hat{\epsilon_1}$ (in the ground frame) and the motion is counterclock-wise as seen from above.

38. A small body is placed on an incline which is pointed along the southern - northern  direction. Find the angle of inclination below which the body will slide up the plane neglecting  friction. Assume the incline is located at latitude $\lambda$.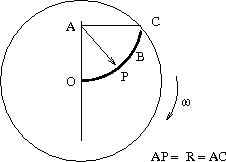



39. A particle of mass $m$ is moving frictionlessly along a circular slot OPBC of radius $R$. The slot is made on a disk (centre $O$) which is moving with a uniform angular velocity $\omega$  It starts from rest when the $\angle{OAP}\,=\,\theta\,=\,0 $ (that is from $O$).

1. Find the force exerted by the slot on the particle as a function of $\theta$.
2. Find the speed $u$ of the particle relative to the slot just as it reaches $C$.

40. Consider a particle having an initial velocity $\vec{V}_0 $ ( say a bullet being fired from  the earth's surface) at a latitude $\lambda$. Assuming the rotation of the is constant ($\frac{d\vec{\Omega}}{dt}\,=\,0$) we have the equation for the motion of the particle is given by (in the rotating frame of the earth) $$ \frac{d^2\vec{r}}{dt^2}\ =\ -2(\vec{\Omega}\times\frac{d\vec{r}}{dt}) \ +\vec{g}_{eff}\ \ \rm{Equation} (A)$$ where $$ \vec{g}_{eff}\ =\ \vec{g}\, -\vec{\Omega}\times(\vec{\Omega}\times\vec{r}) $$

1. Show that in the rotating frame ( show $-\vec{\nabla}V_{eff}\,=\,m\vec{g}_{eff}$ ), where $V_{eff}$ is given by $$ V_{eff}\ =\ V\ - \ \frac{m}{2} (\vec{\Omega}\times\vec{r}).(\vec{\Omega}\times\vec{r}) $$ and  $V\,=\, -m\vec{g}.\vec{r}$.
2. Show that $$ \vec{r}(t)\ +\ \vec{r}(t=0)\ +\ \vec{v}(t=0)t \ +\ \frac{\vec{g}_{eff}\,+\,2\,(\vec{v}(t=0)\times\vec{\Omega})t^2}{2}\,+\,\frac{1}{3}(\vec{g}_{eff}\times\vec{\Omega})t^3 $$ upto order $g\,\vec{\Omega}\,t^3$.

NOTE: If we assume $\vec{g}_{eff}$ is constant, Equation $(A)$ can be solved exactly. The answer is $$ \vec{r}(t)\ =\ \vec{r}(t=0)\ +\ \vec{v}(t=0)t \ +\ \frac{\vec{g}_{eff}t^2}{2}\,+\, \frac{(\rm{cos}(2\Omega t)\,-1)}{2\Omega^2}(\vec{\Omega}\times\vec{v}_0)$$
$$\,-\,\frac{1-2\Omega^2\,t^2-\rm{cos}(2\Omega t)}{4\Omega^4}[\vec{\Omega}\times(\vec{\Omega}\times\vec{g}_{eff})]$$
$$-\frac{2\Omega\,t-\rm{sin}(2\Omega t)}{2\,\Omega^3}[\frac{1}{2}(\vec{\Omega}\times\vec{g}_{eff})\,-\, \vec{\Omega}\times(\vec{\Omega}\times\vec{v}(t=0)] $$
Try and get it (not for submission).
Will be happy to discuss with you on how to obtain this expression.