CMI CM-I Problem Sheet 5 (2012)

21. Show that ( using the notation in the class) the motion of a planet in an ellptical orbit satsfies the following equation
$$ t\, -\, t_0\ =\ (\frac{\mu}{2Gm_1m_2})^{1/2}\,\int_{r_0}^{r}\frac{r'dr'}{(r'-\frac{a(1-e^2)}{2}-\frac{r'^2}{2a})^{1/2}} $$
where $r_0,r$ denote the r-coordinate of the planet at times $t_0,t$ respectively.

Substituting $r\,=\,a(1\, -\,e\rm{cos}(\psi)) $ perform the integral and obtain
$$ t\,-\,t_0\ =\ (\frac{\mu a^3}{Gm_1m_2})^{1/2}[(\psi\,-\, \rm{e}\,\rm{sin}(\psi))\,-(\psi_0\,-\,e\,\rm{sin}(\psi_0))]$$

Show that the angle $\psi$ corresponds to the angle in the figure.

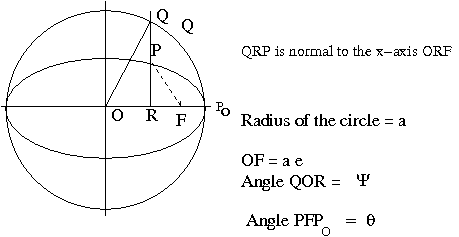
Show that the angle $\psi $ represnted in the figure is the same as in the above definition.

22. Referring to the previous problem $\psi\,-\rm{sin}(\psi)\,=M$ is called the mean anomaly in astronomy. Kepler obtained this result using only geometry and his first law which states that planet sweeps equal area in equal time. Reproduce the argument of Kepler - first show
$$ \frac{\rm{Area\  of\  the\  sector}(FPP_0)}{\pi ab}\,=\, \frac{\rm{Area\  of\  the\  sector}(FQP_0)}{\pi a^2}$$
$$ =\frac{1}{\pi a^2}[ \rm{Area\  of\  the\  circular\ sector}(OQP)-\rm{Area\  of\  the\  triangle}(OQF)]$$
$$ =\  \frac{1}{2\pi } (\psi-e\,\rm{sin}(\psi))\ =\ \frac{t-t_0}{T} $$
Here $T$ is the time taken to complete one orbit.

23. Show that the Runge-Lenz's vector
$$ \vec{K} \ =\ \vec{v}\times\vec{J}\,-\,\frac{Gm_1m_2}{r}\vec{r}$$
where $\vec{J}$ is the angular momentum of the particle about the origin ( the centre of force) is a constant of motion for a particle moving under a gravitational force. Find the relation between the vector $\vec{K}$ and the vector  $\vec{e}$ defined in the class.

24. A comet is in a orbit around the sun has a velocity of 10km/sec. at aphelion ( farthest point from the sun) and 80 km/sec at perihelion ( closest point ot the sun). If the earth's velocity treated as a circle of radius $1.5\times 10^8 $km. and it's orbital speed as $30 $ km/sec., find the aphelion distance $R$ of the planet from the Sun ( Focus).

25. Consider a spacecraft to be launched from the earth to the planet mars. Assume the orbit of the space craft is such that it starts from  earth at it's perihelion and when it reaches mars it is at its aphelion. ( Assume all the orbits ( earth's, mar's and the spacecraft's) lie in a plane. Find the time needed for the space craft to reach mars from  earth.
Mean distance of the earth from  sun/Mean distance of mars from  sun =1/1.5. Treat the earth's and the Mars orbit as circular.

In what direction should the launch be made from earth for minimum expenditure of fuel?