CMI CM-I Problem Sheet 3 (2012)

11. An electron moving with an intital velocity enters an electric field $E(t)\hat{\epsilon}_1$ with a velocity $V_0\cap{\epsilon}_1$. The acceleration is given by $\vec{a}\,=\, eE(t)\hat{\epsilon}_1/m$, where $m$ is the mass of the electron.
The magnitude of the electric field is given by
$$ E(t)\ =\ 0 \ for\  t<0; E(t)\ =\ \frac{E_0t}{\tau} \ for 0\,<\,t\, <\tau \,;$$
$$ E(t)\ =\ \frac{E_0}{\tau} ( t-\tau) \, for \, \tau<t\, <2 \, \tau ;$$
$$ E(t+2\tau)\ =\ E(t) \ t\,>\,0 $$
Find the distance travelled in time $n\tau$, $n$ being an integer..

12. Consider a damped harmonic oscillator described by
$$ m\frac{d^2x}{dt^2}\,+\,\lambda \frac{dx}{dt}\,+\, k\,x\,=\,0 $$
with $x(t=0)=A$ and $\frac{dx}{dt}|_{t=0}\,=\,0$. Calclate the average value of the total energy $ <E>_{nT}$  over a cycle $nT\,\leq \, t \, \leq (n+1)T$, after $n$ cycles. T is the time period. Use the result to show
$$  <E>_{nT}\,=\, <E>_{0}\,e^{-2\gamma nT} \ for\  \gamma\,<<(\frac{k}{m})^{1/2}$$
where $\gamma=\lambda/(2m)$.

13. Find the equilibrium position and the frequency of small oscillations about the equilibrium position for the potential
$$ V(x)\ =\ -\frac{a}{x^6}\,+\,\frac{b}{x^{12}} $$
where $a,b$ are positive constants.

14. The Seismograph: This instrument is used in recording disturbances within the earth, such as those created in earthquakes. The instrument is a spring mass system with a resistance term proportional to the velocity. See figure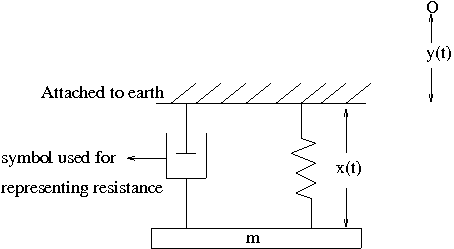



Let $y(t)$ be the displacement of the platform with respect $O$, origin in an inertial frame. $x(t)$ is the displacement of the mass $m$ with respect to the platform. If $y(t)\,=\, A\,\rm{cos}(\Omega t) $ show that
$$ x(t)\ =\ \frac{mg}{k} \,+ \, L\, + \frac{A\rm{cos}(\Omega t+\phi)\Omega^2}{(\omega^2[(1-\frac{\Omega^2}{\omega^2})^2+\frac{4\gamma^2\Omega^2}{\omega^4}])^{1/2}} $$
where
$$ \rm{tan}(\phi)\ =\ \frac{2\gamma\Omega}{\Omega^2-\omega^2} $$
$L,k $ is the natural length of the spring ( massless) and the spring constant respectively  , $\omega^2\,=\,k/m$. If the spring is soft
$$ \frac{\omega}{\Omega}\,\rightarrow\, 0$$,
 show that when $\gamma/\Omega\,<<1$
$$ x(t)\ =\  \frac{mg}{k}\,+\,L\, A \rm{cos}(\Omega t+\phi) $$
Thus
$$\eta \ = \ x(t)\,-L\,-\frac{mg}{k} \ \propto\ A$$
the amplitude of the forced oscillation which is what the Seismograph measures..

Further if $\frac{\omega}{\Omega} \,>>\,1 $, $\eta\,\propto\, A\Omega^2 $ which measures the acceleration fo the platform. Thsi is the principle of the accelerometers used in aircrafts.

15. Consider a mass $m$ moving under a simple harmonic force ( force constant $k\,= m\omega^2$ ) with dry friction ( Force of friction = Normal reaction X coeffficient of friction ). Taking the normal reaction as $mg$ and $ \mu$ as the coefficient of friction discuss the motion. Assume an initial state at $t=0$ as $ x(0) = A \,;\, \frac{dx}{dt}(0)=0$. Consider $A $ in the range $ 0.5\mu\, mg/k\  to\  2.5\mu\, mg/k$.