CMI CM-I Problem Sheet 2 (2012)

6. A force law of a body falling in air is given by $$ \vec{F}=-mg\hat{k}-C\vec{v}$$ where $\vec{v}$ is the velocity of the particle. and $C$ is a constant.

(a) Obtain the equation of motion in the $x-$ direction and solve for $v_x$ as a function of $t$, given at $t=t_0, v_x=v_0$
(b) Repeat the same for $z-$ direction. In particular solve for $v_z$ as a function of $t$, given at $t=t_0, v_z=u_0$
( $\hat{i},\hat{j} \,\rm{and} \,\hat{k}$ are unit vectors along x,y and z directions)

7. Consider the setup shown in the figure - ABCD is rigid set of massless rods which can oscillate about A on a stand X fixed to the ground. The rods BC and BD make a constant angle $\alpha$ with respect to rod AB. Two masses M are attached at C and D of the rods BC and BD respectively. $\rm{AB}=\,K;\, \rm{BC}\,=\,\rm{BD}\,=\,L$. Find the potential energy of the set of rods (along with the masses attached) as a function of the angle made  by AB with the vertical (label the angle as $\theta$). Show that the oscillations of the rigid set is stable if $ L\,\rm{cos}(\alpha)\,>\, K$.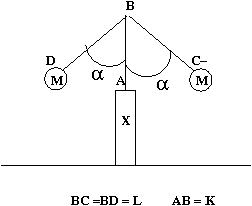


8. Obtain an expression for the displacement vector $\vec{r}$ for an aircraft circling above an air field at a height H in a circle of radius R with constant speed U. Choose $\hat{\epsilon}_3 $ as a unit vector along the vertical. You can choose any point for the initial position of the aircraft - specify it and the centre of the circle as $(0,0,\rm{H})$.

9. The velocity of a particle moving along the x- axis is given by  
$$ v^2(t)\,=\,\frac{K}{x(t)} $$
where $K$ is a constant and $x(t)$ is the distance travelled in time $t$. Given $v(o)\,=\,U$ find $v$ as a function of $t$

10. The acceleration of atomic particles to large velocities  in a linear accelerator is obtained by using an alternating radio frequency voltage. The particles are accelerated in region 1 and 2, leaving 1 at time $t_1$ and reaching 2 at $ t_2$. It has constant velocity $v_1$ in the region 1 and $v_2$ in 2.Between region 1 and 2 ( in the gap) the particle is accelerated at $a\,=\, a_0\rm{sin}(\omega t)$, where $a_0$ is a constant. Given $t_1\,=\, T/8,t_2\,=\,3T/8$ where $T=(2\pi)/\omega$.
Further the particle leaves region 2 at $t_3=9T/8$. Find th length of the gap between the two regions and length of the region 2.