[NOTES/CM-08013] Rotation of a Vector about \(X_3\)- Axis

Rotating the vector
Consider clockwise rotation of a vector by an angle \(\alpha\) see \Figref{Fig1A}. Let the position vector of point \(P\) be \(\vec x =(x_1, x_2, x_3)\) and that of \(P\Prime\) be \(\vec x\Prime =(x_1\Prime, x_2\Prime, x_3\Prime)\). Because the rotation is about the \(X_3\) axis we have \(x_3=x_3\Prime\). Letting \(R\) denote the distance of \(P\) and \(P\Prime\) from the origin. The required relation is easy to derive if we work the complex numbers \(z, z\Prime\) defined by \begin{equation} z=x_1+ix_2, \qquad z\Prime=x_1\Prime+ix_2\Prime. \end{equation} The complex numbers \(z\) and \(z\Prime\) have polar representations in terms of angles \(\theta, \alpha\) as given below. \begin{equation} z= R e^{i\theta}, \qquad z\Prime= Re^{i(\theta-\alpha)}. \end{equation} Considering real and imaginary parts of \(z\) and \(z\Prime\) we have
\begin{equation}\Label{EQ03} x_1= R \cos\theta, \quad x_2 = R\sin\theta \end{equation}
The complex numbers \(z\Prime\) is related to \(z\) by a phase, \(z\Prime =e^{i(\theta-\alpha)}\). Taking real and imaginary parts, we get \begin{equation}\Label{EQ04} x_1\Prime =R \cos(\theta-\alpha), \quad x_2\Prime =R \sin(\theta-\alpha). \end{equation}
Expanding the sine and cosines in \eqref{EQ04} and using \eqref{EQ03}, we get
\begin{eqnarray}\Label{EQ05} x_1\Prime &=&R \cos\theta\cos\alpha + R\sin\theta \sin\alpha = x_1 \cos\alpha + x_2 \sin\alpha\\ x_2\Prime &=& R \sin\theta \cos\alpha -R \cos \theta \sin\alpha = x_2\cos \alpha - x_1 \sin\alpha \Label{EQ06} \end{eqnarray}

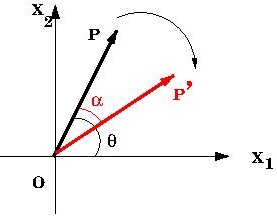Fig 1. Rotation of Vectors The figure shows a vector \({\overrightarrow{OP}}^\prime\) obtained by a clockwise rotation of vector \(\overrightarrow{OP}\) by a {\sl clockwise rotation} by an angle  \(\alpha\) about the \(X_3\) axis.

Rotating the coordinate system:
Let \(K\Prime\) be a system of axes related by a rotation about the \(X_3\) axis of  system  \(K\) by an angle \(\alpha\). The positive sense of rotation is given by the right hand rule.

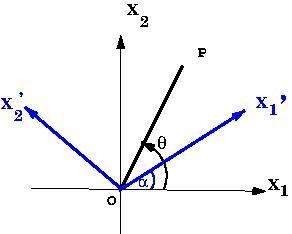Fig 2 Rotation of coordinate axes. Under an  anti clockwise rotation by an angle \(\alpha\) about the \(X_3\) axis, the axes \(X_1\)-\(X_2\) go over to \(X_1^\prime\)--\(X_2^\prime\).

Making use of complex numbers again, we can writing the polar form of coordinates for the point \(P\) in two different ways. With respect to the first set of axes \(X_1\)-\(X_2\), coordinates of the point \(P\) are

\begin{equation}\label{EQ47} z\equiv x_1 +  i x_2 = R e^{i\theta}. \end{equation}

Next we write the same complex number \(z\) in terms of a polar form w.r.t the primed axes and  get
\begin{equation}\label{EQ48} z\Prime\equiv x_1\Prime +  i x_2\Prime = R e^{i(\theta-\alpha)}. \end{equation}
Using the fact that the complex numbers \(z\) and \(z\Prime\),  represent the same point \(P\). Equations \eqref{EQ47} and \eqref{EQ48}, after some manipulations in complex numbers, gives

\begin{eqnarray}
x_1\Prime &=& R\cos(\theta-\alpha) =R \cos\theta\cos\alpha + R\sin\theta \sin\alpha\\
&=& x_1 \cos\alpha + x_2 \sin\alpha   \label{EQ09}\\
x_2\Prime &=& R\sin (\theta-\alpha)\nonumber = R \sin\theta \cos\alpha -R \cos \theta \sin\alpha\\
&=& x_2\cos \alpha - x_1 \sin\alpha \label{EQ10} \end{eqnarray}
The above relations give the desired transformation rules relating components of position vector of a point in coordinate system \(K\) and rotated system \(K^\prime\).

The relations \eqref{EQ09} and \eqref{EQ10} coincide with the relations \eqref{EQ05} and \eqref{EQ06}, respectively. The result obtained in the above, can be summarized  as follows. 

• It must remembered that the quantities \(\vec x\equiv(x_1, x_2,x_3)\) and \(\vec x\Prime \equiv (x_1\Prime,x_2\Prime,x_3\Prime)\) and have different meanings in the two cases.In the first case \(\vec x\) and \(\vec x\Prime\) represent the original and the rotated vectors, before and after the rotation respectively. In the second case the quantities \((x_1, x_2,x_3)\) and \((x_1\Prime,x_2\Prime,x_3\Prime)\) represent the components of the {\sl same} vector w.r.t to two  different sets of axes.
• Rotating the coordinate axes is equivalent to rotating the vector in the opposite direction in the sense that the relations between the components of \(\vec x\) and \(\vec x\Prime\) are the same in the two cases. This is most easily seen by noting that in both cases \(z\Prime= e^{-i\alpha}z\).