[NOTES/CM-08005] Finite Rotations of Vectors about an Arbitrary Axis

In this section a rotation will mean rotation of vectors with the coordinate axes remaining fixed. Let \(\vec{A}=(A_1,A_2,A_3)\) and \(\vec{A}'=(A_1',A_2',A_3')\) denote a vector and rotated vector. We will derive the result \begin{equation}\label{EQ01} \vec{A}^\prime = \vec{A} - (\hat{n}\times\vec{A})\, \sin\alpha + \hat{n}\times (\hat{n}\times\vec{A})\, (1-\cos\alpha ) \end{equation} by geometrical arguments. The transformation equation of every vector, under a chosen rotation, is the same as those for the position vector of points under the rotation. In the figure below $OX$ represents the axis of rotation. Under a clockwise rotation, a vector $\overrightarrow{OP}$ moves to the vector $\overrightarrow{OQ}$. The point $P$ moves on arc of a circle, lying in the plane perpendicular to the axis of rotation, and goes to a point $Q$. The centre of the circle, $N$, lies on the axis of rotation. The angle of rotation $\alpha $ is the angle $\angle PNQ$. The vector $\overrightarrow{PQ}$ is the difference between the vector $\overrightarrow{OP}$ and the rotated vector $\overrightarrow{OQ}$. A proof of the result \eqref{EQ01} will be broken into following steps.

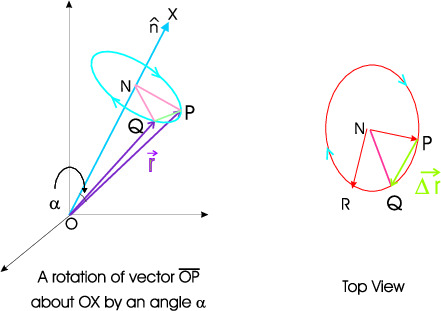
1. Draw a radius $NR$ perpendicular to $NP$ as shown in the top view diagram.
2. Using \(\vec r\) and \(\vec r\Prime\) to denote the position vectors of the point \(P\) and \(Q\), respectively. we can now verify \begin{eqnarray} \vec{r} &=& \overrightarrow{ON}+\overrightarrow{NP}.\\ \vec{r}^\prime &=& \overrightarrow{ON}+\overrightarrow{NQ}, \label{EQ03}\\ &=& \overrightarrow{ON}+\overrightarrow{NP} + \overrightarrow{PQ}. \end{eqnarray}
3. In view of the fact that \(\hat{n}\) is a vector along \(\overrightarrow{ON}\), we get \begin{eqnarray} \hat{n}\times \vec{r}&=& \hat{n}\times \overrightarrow{NP},\\ \hat{n}\times \vec{r}^\prime&=& \hat{n}\times \overrightarrow{NQ}. \end{eqnarray}
4. We can resolve the vector $\overrightarrow{NQ}$ along two perpendicular directions $NP$ and $NR$. Let \(\hat{\ell}\) denote unit vector along $\overrightarrow{NR}$ and \(\hat{m}\) be a unit vector along \(\overrightarrow{NP}\). Then we have \begin{eqnarray} \hat{\ell}&=& \frac{\overrightarrow{NR}}{NR}, \qquad \overrightarrow{NR}=(NR) \hat{\ell}.\\ \hat{m} &=& \frac{\overrightarrow{NP}}{NP}, \qquad \overrightarrow{NP} = (NP) \hat{m}. \end{eqnarray}
5. The three unit vectors \(\hat{\ell},\hat{m}, \hat{n}\) fo arm mutually orthogonal right handed system. In fact from the diagram it is seen that \begin{equation} \hat{\ell}\times\hat{m}=\hat{n};\quad \hat{m}\times\hat{n}=\hat{\ell};\quad \hat{n}\times \hat{\ell}=\hat{m}. \end{equation}
6. We resolve the vector \(\overrightarrow{NQ}\) as a sum of unit vectors \(\hat{\ell}, \hat{m}\). Now \(\angle QNP\) is equal to the angle of rotation \(\alpha \). Hence \begin{eqnarray}\nonumber \overrightarrow{NQ} &=& NQ \cos\alpha \, \hat{m} + NQ \sin \alpha \, \hat{\ell}\\\nonumber &=& NP \cos\alpha \, \hat{m} + NR \sin \alpha \, \hat{\ell}\\ &=& \overrightarrow{NP}\, \cos\alpha + \overrightarrow{NR}\, \sin\alpha \label{EQ10} \end{eqnarray} Next we express the vectors \(\overrightarrow{NP}\) and \(\overrightarrow{NR}\) in terms of cross products of \(\hat{n}\) and \(\vec{r}\). We have \begin{eqnarray}\label{EQ11} \hat{\ell} = \hat{m}\times \hat{n} \Longrightarrow \frac{\overrightarrow{NR}}{NR}= \frac{\overrightarrow{NP}}{NP}\times\hat{n} \end{eqnarray} Since \(NP=NR\), we get \begin{eqnarray}\label{EQ12} \overrightarrow{NR} = \overrightarrow{NP}\times\hat{n} = (\hat{n}\times \vec{r})\times \hat{n}=-\hat{n}\times(\hat{n}\times\vec{r}). \end{eqnarray} Similarly, \begin{eqnarray}\nonumber \overrightarrow{NP} &=& NP (\hat{m})= NP (\hat{n}\times \hat{\ell}) = NR (\hat{n}\times \hat{\ell}) = (\hat{n}\times \overrightarrow{NR})\\\nonumber &=&\hat{n}\times( \hat{n}\times (\hat{n}\times\vec{r})) =\hat{n}\times[ \hat{n} (\hat{n}\cdot\vec{r}) -\vec{r} ]\\ &=&- (\hat{n} \times \vec{r}).\label{EQ13} \end{eqnarray}
7. Substituting \eqref{EQ12} and \eqref{EQ13} in \eqref{EQ10}, we get \begin{equation} \overrightarrow{NQ} = - \hat{n}\times(\hat{n}\times\vec{r})\, \cos\alpha - (\hat{n} \times \vec{r}) \sin \alpha . \end{equation} The above result, when used in \eqref{EQ03}, gives \begin{eqnarray} \vec{r}\Prime = (\hat{n}\cdot \vec{r}) \hat{n} -(\hat{n}\times \vec{r}) \sin\alpha - \hat{n}\times(\hat{n}\times \vec{r})\cos\alpha .\label{EQ15} \end{eqnarray} Making use of \[ (\hat{n}\cdot \vec{r}) \hat{n} = \hat{n}\times(\hat{n}\times \vec{r}) +\vec{r},\] \eqref{EQ15} can be rearranged to give the following alternate form \begin{eqnarray} \vec{r}\Prime = \hat{r} -(\hat{n}\times \vec{r}) \sin\alpha + \hat{n}\times(\hat{n}\times \vec{r})(1-\cos\alpha ) . \end{eqnarray}
8. Thus a vector \(\vec{A}\), under rotation by an angle \(\alpha \), coincides with a vector \(\vec{A}\Prime\) given by \begin{equation} \boxed{ \vec{A}\Prime = \vec{A} -(\hat{n}\times \vec{A}) \sin\alpha + \hat{n}\times(\hat{n}\times \vec{A})(1-\cos\alpha )} \end{equation}