$\newcommand{\Prime}{^{\prime}}$
Euler angles are an important ways of parametrization of rotations. The definition of Euler angles and and expression of the rotation matrix in terms of the Euler angles are given.
The Euler angle parametrization of rotations is very useful in visualization of
the solution of the EOM for a rigid body.
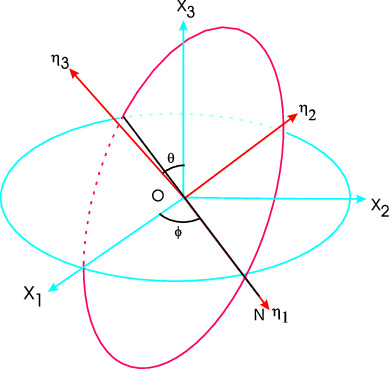
Let $OX_1,OX_2,OX_3$ (shown in blue) and $O{X_1}\Prime,O{X_2}\Prime,O{X_3}\Prime$ (shown in red) be two sets of coordinate axes related by a rotation. The orientation of ${K\Prime}$ system , relative to $K$, can be completely and uniquely specified in terms of three angles called Euler angles. To define the Euler angles, consider line of intersection of $(X_1,X_2)$ and $(X_1\Prime,X_2\Prime)$ planes. Let us assume that this line, called the line of nodes, makes an angle $\phi$ with $OX_1$ and an angle $\psi$ with ${X_1}\Prime$. Let $\theta$ be the angle between the axes $OX_3$ and $O{X_3}\Prime$. The three angles $(\phi,\theta,\psi)$, so defined, are called Euler angles.

Warning
Different books use different definitions of the Euler angles. Our definition is the same as that in Goldstein.
If the two sets of axes \(K\) and \(K\Prime\) are known, we can obtain the three Euler angles. Conversely, if the three Euler angles are given the set ${K}\Prime$ of ${X_1}\Prime,{X_2}\Prime,{X_3}\Prime$ axes may be obtained by applying three successive rotations as explained below.
First rotation:
We first rotate the about $X_3$ by angle $\phi$ to get the $\xi_1,\xi_2,\xi_3$ axes, noting that $\xi_3$ will be same as $X_3$ and now $\xi_1$ coincides with the line of nodes, see figure below.
 |
 |
 |
Second rotation
The next rotation is about the line of nodes, {\it i.e.} about $\xi_1$ by angle $\theta$, giving the new axes $\eta_1,\eta_2,\eta_3$. After this rotation $\xi_2$ axis coincides with $\eta_2$ and $X_3$ moves to $\eta_3$ which is the final $\equiv X_3\Prime$ axis.
Third rotation
The third and final rotation is about $\eta_3$ by angle $\psi$, giving the axes $={X_1}\Prime,{X_2}\Prime,{X_3}\Prime$. After this transformation $\eta_3$ axis remains ${X_3}\Prime$ axis, $\eta_1$ moves to ${X_1}\Prime$, $\eta_2$ moves to new position ${X_2}\Prime$
The rotation matrix in terms of the Euler angles is
\begin{equation}
R = R_3(\psi) R_1(\theta) R_3(\phi). \label{EQ63}
\end{equation}
Here $R_1, R_3$ represent the rotation matrices about the first and the third axes. Explicitly, we have
\begin{eqnarray} R_3(\phi) &=& \left[ \begin{array}{rrr}\cos \phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{array}\right] \\R_1(\theta) &=& \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \cos \theta & \sin\theta \\ 0 & -\sin\theta & \cos\theta \\ \end{array} \right] \\ R_3(\psi) &=& \left[ \begin{array}{rrr} \cos \psi & \sin\psi & 0 \\-\sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{array} \right] .\end{eqnarray}






 ||Message]
||Message]
