[NOTES/CM-06007] Hard Sphere Scattering

We first compute the scattering angle of a beam scattered from a hard sphere represented by the potential
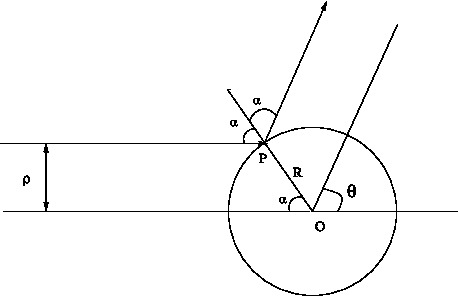
\begin{equation} V(r) =\begin{cases} 0 & r> R\\ \infty & r< R \end{cases} \end{equation}The situation is shown in figure below.

Hard sphere scattering

The scattering angle is related to the angle \(\alpha\) by

\begin{equation}\theta = \pi -2\alpha, \Rightarrow \alpha = \pi/2 -\alpha.\end{equation}Therefore the impact parameter $\rho$ is given by\begin{equation} \rho = R \sin \alpha = R \cos(\frac{\theta}{2})\end{equation}Hence the differential cross section is\begin{eqnarray} \sigma(\theta) &=& \frac{\rho}{\sin\theta} |\frac{d\rho}{d\theta}|\\ &=&\frac{R \sin(\frac{\theta}{2})R \cos(\frac{\theta}{2})}{\sin\theta} \times \frac{1}{2}\\ &=& \frac{1}{4}R^{2} \end{eqnarray} and the total cross section is found to be
\begin{eqnarray} \sigma_{t} = \int_{0}^{\pi} 2\pi \sin\theta \sigma(\theta) d\theta =\int_{0}^{\pi} 2\pi \frac{R^{2}}{4} \sin\theta d\theta =\frac{\pi R^{2}}{2} \int_{-1}^{1} dt = \pi R^{2}. \end{eqnarray}Therefore we get the total cross section for hard sphere scattering as\begin{equation}
\sigma_{t} = \pi R^{2}/\end{equation}