[NOTES/CM-06006] Computation of Cross Section

Formula for scattering cross section
We shall derive a relation between the different scattering cross section and the scattering angle as function of impact parameter.

Consider motion of a particle of energy $E$ in a spherically symmetric potential $V(r)$ produced by the target.

Let the angular momentum of the particle be $L$, initial velocity $V_0$ and scattering angle $\theta$. Then
\begin{equation}
L={\mu}{v_0}{b} =\sqrt{2\mu E}{\rho}
\end{equation}
Solution of equations of motion gives the scattering angle $\theta$ as a function of impact parameter $b$ and energy $E$
\begin{equation}
\theta=\theta(E,b).
\end{equation}
If the impact parameter is increased by a small amount $db$, the change in scattering angle is given by
\begin{equation}
d{\theta}=\frac{d\theta}{db} {db} .
\end{equation}
The range $\theta, \theta+d\theta$ for the scattering angle corresponds to a solid angle $d\Omega$, 
\begin{equation}
d\Omega=2\pi \sin\theta{d}\theta \qquad\qquad
\end{equation}

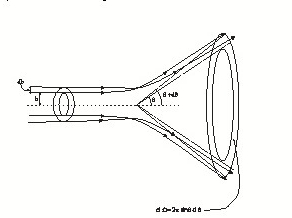Fig.1 The range $(\theta,\theta+d\theta)$ of angle corresponds to $(b, b+db)$} of impact parameter

For spherically symmetric potential cross section will be independent of $\phi$. Now we have

Using the definition of flux, the left hand side of (A) is
\begin{equation}
\text{L.H.S }=\text{Flux} \times{2}\pi{b}{db} \label{EQ06}
\end{equation}
R.H.S of (A), using the definition of $\sigma_t$ is

\begin{eqnarray} \text{R.H.S. } &=&{\sigma_t}\times {d \Omega} \times \text{Flux}\\
&=&{\sigma_t}\times\text{ Flux }\times{2}\pi{\sin\theta}{d\theta}\label{EQ08} \end{eqnarray}

Equating \eqref{EQ06} and \eqref{EQ08} we get

\begin{equation}
{\sigma_t}=\frac{b}{\sin \theta} \frac{db}{db}
\end{equation}
Since $\sigma_t$ is always positive where as $\frac{db}{d\theta}$ may be positive or negative. Therefore, we write
\begin{equation}
\sigma_t=\frac{\rho}{\sin\theta}\Big|\frac{db}{d\theta}\Big|.
\end{equation}